Question

11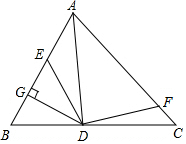．已知：如图所示，在△ABC中，AD是△ABC的角平分线，E、F分别是AB，AC上的点，并且有∠EDF+∠EAF=180°，DG⊥AB于点G．
（1）试判断DE和DF的数量关系，并说明理由；
（2）若△ADF和△AED的面积分别为50和39，求△EDG的面积．

Answer 1

分析 （1）过D作DM⊥AB，于M，DN⊥AC于N，根据角平分线性质求出DN=DM，根据四边形的内角和定理和平角定义求出∠AED=∠CFD，根据全等三角形的判定AAS推出△EMD≌△FND即可；
（2）作DM=DE交AC于M，作DN⊥AC，利用角平分线的性质得到DN=DG，将三角形EDG的面积转化为三角形DNM的面积来求．

解答 （1）证明：过D作DN⊥AC于N，∵DG⊥AB于点G，
∴∠EGD=∠FND=90°，
∵AD平分∠BAC，DG⊥AB，DN⊥AC，
∴DG=DN（角平分线性质），
∵∠EAF+∠EDF=180°，
∴∠AED+∠AFD=360°-180°=180°，
∵∠AED+∠DEG=180°，
∴∠GED=∠NFD，
在△EGD和△FND中
$\left\{\begin{array}{l}{∠GED=∠DFN}\\{∠DGE=∠DNF}\\{DG=DN}\end{array}\right.$，
∴△EMD≌△FND（AAS），
∴DE=DF；

（2）解：作DM=DE交AC于M，
∵DE=DF，DM=DE，
∴DM=DF，
∵AD是△ABC的角平分线，DG⊥AB，
∴DG=DN，
在Rt△DEG和Rt△DMN中，
$\left\{\begin{array}{l}{DN=DG}\\{DM=DE}\end{array}\right.$，
∴△DEG≌△DNM（HL），
∵△ADF和△AED的面积分别为50和39，
∴S_△MDF=S_△ADF-S_△ADM=50-39=11，
S_△DNM=S_△DEG=$\frac{1}{2}$S_△MDG=$\frac{1}{2}$=5.5．

点评 本题考查了角平分线的性质及全等三角形的判定及性质，解题的关键是正确地作出辅助线，将所求的三角形的面积转化为另外的三角形的面积来求．