题目内容
设二次函数y=x2+2(cosθ+1)x+cos2θ,(0<θ≤90°)的图象与x轴两交点的横坐标分别为x1,x2,并且|x1-x2|≤2
,则θ的取值范围是 .
| 2 |
考点:抛物线与x轴的交点,根的判别式,根与系数的关系,锐角三角函数的增减性
专题:数形结合
分析:根据根与系数的关系,建立cosθ与两根的和与积的关系,再将|x1-x2|≤2
两边平方,得到关于两根积与两根和的关系式,
再将cosθ与两根的和与积的关系式代入求解.
| 2 |
再将cosθ与两根的和与积的关系式代入求解.
解答:解:∵x1+x2=-2(cosθ+1),x1x2=cosθ,
又∵|x1-x2|≤2
,
∴(x1+x2)2-4x1x2≤8,
∴4(cosθ+1)2-4cos2θ≤8,cosθ≤
,
又∵△=4(cosθ+1)2-4cos2θ>0,
∴4(2cosθ+1)>0(0°<θ≤90°)总成立.
∴cosθ≤
,
故答案为:60°≤θ≤90°.
又∵|x1-x2|≤2
| 2 |
∴(x1+x2)2-4x1x2≤8,
∴4(cosθ+1)2-4cos2θ≤8,cosθ≤
| 1 |
| 2 |
又∵△=4(cosθ+1)2-4cos2θ>0,
∴4(2cosθ+1)>0(0°<θ≤90°)总成立.
∴cosθ≤
| 1 |
| 2 |
故答案为:60°≤θ≤90°.
点评:此题主要考查了根与系数的关系和抛物线与x轴的交点坐标与两点之间的距离的关系,解答时要考虑cosθ的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
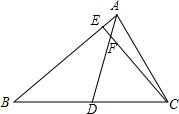 如图,△ABC中,AD是BC边上的中线,F是AD上一点,有AF:FD=1:5,连接CF,并延长交AB于E,则AE:EB等于( )
如图,△ABC中,AD是BC边上的中线,F是AD上一点,有AF:FD=1:5,连接CF,并延长交AB于E,则AE:EB等于( )| A、1:6 | B、1:8 |
| C、1:9 | D、1:10 |
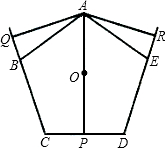 如图,ABCDE是正五边形,从顶点A向三边BC、CD、DE(或其延长线)作垂线AQ、AP、AR、(Q、P、R是垂足),O是此五边形的中心,若OP=1,求AO+AQ+AR的值.
如图,ABCDE是正五边形,从顶点A向三边BC、CD、DE(或其延长线)作垂线AQ、AP、AR、(Q、P、R是垂足),O是此五边形的中心,若OP=1,求AO+AQ+AR的值. 如图,等腰三角形ABC中,AB=AC,P点在BC边上的高AD上,且
如图,等腰三角形ABC中,AB=AC,P点在BC边上的高AD上,且 如图,长方形ABCD正好被分成6个正方形,如果中间最小的正方形面积等于1,那么长方形ABCD的面积等于
如图,长方形ABCD正好被分成6个正方形,如果中间最小的正方形面积等于1,那么长方形ABCD的面积等于