题目内容
15.观察下列等式:①1-1-$\frac{1}{2}$=-$\frac{1}{1×2}$;
②$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$=-$\frac{1}{3×4}$;
③$\frac{1}{3}$-$\frac{1}{5}$-$\frac{1}{6}$=-$\frac{1}{5×6}$;
④$\frac{1}{4}$-$\frac{1}{7}$-$\frac{1}{8}$=-$\frac{1}{7×8}$;
…
根据上述规律解决下列问题:
(1)完成第⑤个等式;
(2)写出你猜想的第n个等式(用含n的式子表示)并证明其正确性.
分析 (1)根据题意可得,左边的第2项和第3项的分母分别是连续的奇数和偶数,右边的分母为是左边第2项和第3项的分母之积,由此可得第5个等式;
(2)根据(1)中的规律,用含n的代数式表示,再利用分式的运算进行证明.
解答 解:(1)∵左边的第2项和第3项的分母分别是连续的奇数和偶数,右边的分母为是左边第2项和第3项的分母之积,
∴第5个等式为:$\frac{1}{5}$-$\frac{1}{9}$-$\frac{1}{10}$=-$\frac{1}{9×10}$;
(2)第n个等式为:$\frac{1}{n}$-$\frac{1}{2n-1}$-$\frac{1}{2n}$=-$\frac{1}{2n(2n-1)}$,
证明:左边=$\frac{2(2n-1)-2n-(2n-1)}{2n(2n-1)}$=-$\frac{1}{2n(2n-1)}$,
右边=-$\frac{1}{2n(2n-1)}$,
∴左边=右边,
∴原式成立.
点评 本题主要考查了规律猜想型问题,关于等式的规律探索:用含字母的代数式来归纳,注意字母往往还具有反映等式序号的作用.

练习册系列答案
相关题目
6.下列各数中,是无理数的一项是( )
| A. | -1 | B. | $\sqrt{2}$ | C. | $\frac{2017}{4}$ | D. | 3.14 |
3.下列判断不正确的是( )
| A. | 如果$\overrightarrow{AB}$=$\overrightarrow{CD}$,那么|$\overrightarrow{AB}$|=|$\overrightarrow{CD}$| | B. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | ||
| C. | 如果非零向量$\overrightarrow{a}$=k•$\overrightarrow{b}$(k≠0),那么$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 |
10.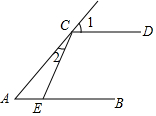 如图,AB∥CD,CE于AB交于E点,∠1=50°,∠2=15°,则∠CEB的度数为( )
如图,AB∥CD,CE于AB交于E点,∠1=50°,∠2=15°,则∠CEB的度数为( )
 如图,AB∥CD,CE于AB交于E点,∠1=50°,∠2=15°,则∠CEB的度数为( )
如图,AB∥CD,CE于AB交于E点,∠1=50°,∠2=15°,则∠CEB的度数为( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
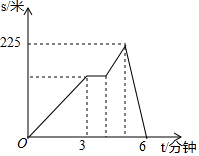 小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.
小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示. 如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)
如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)