题目内容
12.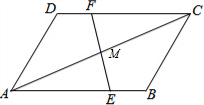 已知:如图,AB∥CD,AD∥BC,E、F分别在AB、CD上,DF=BE,AC与EF相交于点M,求证:AM=CM.
已知:如图,AB∥CD,AD∥BC,E、F分别在AB、CD上,DF=BE,AC与EF相交于点M,求证:AM=CM.
分析 首先证明△ACD≌△CAB,推出AB=CD,由DF=EB,推出FC=AE,再证明△CFM≌△AEM即可.
解答 证明:∵AB∥CD,AD∥BC,
∴∠DAC=∠BCA,∠DCA=∠BAC,
在△ACD和△CAB中,
$\left\{\begin{array}{l}{∠DAC=∠ACB}\\{AC=CA}\\{∠DCA=∠BAC}\end{array}\right.$,
∴△ACD≌△CAB,
∴AB=CD,
∵DF=EB,
∴FC=AE,
在△CFM和△AEM中,
$\left\{\begin{array}{l}{∠FMC=∠AME}\\{∠FCA=∠EAM}\\{CF=AE}\end{array}\right.$,
∴△CFM≌△AEM,
∴CM=AM.
点评 本题考查全等三角形的判定和性质,平行线的性质等知识,解题的关键是用了两次全等三角形的证明,属于中考常考题型.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
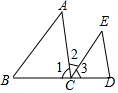 如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.
如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.