题目内容
2.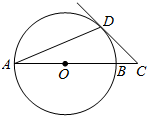 如图,AB是⊙O的直径,且AB=2$\sqrt{2}$,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,则BC的长是( )
如图,AB是⊙O的直径,且AB=2$\sqrt{2}$,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,则BC的长是( )| A. | 2$\sqrt{2}$-2 | B. | $\sqrt{2}$ | C. | 1 | D. | 2-$\sqrt{2}$ |
分析 连接DO,由三角形的外角与内角的关系易得∠DOC=∠C=45°,故有∠ODC=90°,CD=OD=$\frac{1}{2}$AB,在直角△COD中,利用勾股定理即可求解.
解答 解: 连接DO,
连接DO,
∵AO=DO,
∴∠DAO=∠ADO=22.5°.
∴∠DOC=45°.
又∵∠ACD=2∠DAB,AB=2$\sqrt{2}$,
∴∠ACD=∠DOC=45°.
∴∠ODC=90°,CD=OD=$\frac{1}{2}$AB=$\sqrt{2}$,
∴△OCD是等腰直角三角形,
∴OC=$\sqrt{{OD}^{2}+{CD}^{2}}$=$\sqrt{{(\sqrt{2})}^{2}+{(\sqrt{2})}^{2}}$=2,
∴BC=OC-OB=2-$\sqrt{2}$.
故选D.
点评 本题考查的是圆周角定理,根据题意作出辅助线,判断出△OCD的形状是解答此题的关键.

练习册系列答案
相关题目
15.函数y=$\sqrt{x-4}$中自变量x的取值范围是( )
| A. | x≥0 | B. | x>4 | C. | x<4 | D. | x≥4 |
11. 如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )
如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )
 如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )
如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )| A. | 360 | B. | 164 | C. | 400 | D. | 60 |


 如图,一山坡的坡度为i=1:$\sqrt{3}$,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了100米.
如图,一山坡的坡度为i=1:$\sqrt{3}$,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了100米.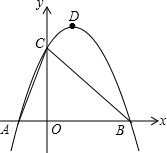 已知:如图,抛物线y=ax2+bx+3交x轴于A(-1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接AC,BC.
已知:如图,抛物线y=ax2+bx+3交x轴于A(-1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接AC,BC.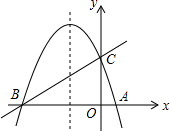 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.