��Ŀ����
18����ͼ�٣��ڡ�ABC�У���ACB=90�㣬��B=30�㣬AC=1��DΪAB���е㣬EFΪ��ACD����λ�ߣ��ı���EFGHΪ��ACD���ڽӾ��Σ����ε��ĸ�������ڡ�ACD�ı��ϣ�����1���������EFGH�������
��2��������EFGH��AB����ƽ�ƣ�F����BC��ʱֹͣ�ƶ�����ƽ�ƹ����У����������CBD�ص����ֵ����Ϊ$\frac{{\sqrt{3}}}{16}$ʱ�������ƽ�Ƶľ��룻
��3����ͼ�ۣ�����2���о���ƽ��ֹͣʱ���õľ��μ�Ϊ����E1F1G1H1��������E1F1G1H1��G1�㰴˳ʱ�뷽����ת����H1����CD��ʱֹͣת������ת��ľ��μ�Ϊ����E2F2G1H2������ת��Ϊ������cos����ֵ��

���� ��1��������֪����ֱ�������ε����ʿ�֪AB=2���Ӷ����AD��CD��������λ�ߵ����ʿɵ�EF��DF���������Ǻ����ɵ�GF���ɾ��ε������ʽ�ɵý����
��2���������÷������۵�˼�룬�������������CBD�ص�����Ϊ������ʱ��$0��x��\frac{1}{4}$�����������Ǻ����������ε������ʽ�ɵý�������������CBD�ص�����Ϊֱ������ʱ��$\frac{1}{4}��x��\frac{1}{2}$�����г����̽��x��
��3����H2Q��AB��Q����DQ=m����${H_2}Q=\sqrt{3}m$����$D{G_1}=\frac{1}{4}$��${H_2}{G_1}=\frac{1}{2}$�����ù��ɶ����ɵ�m����Rt��QH2G1�У��������Ǻ������cos����
��� �⣺��1����ͼ�٣��ڡ�ABC�У�
�ߡ�ACB=90�㣬��B=30�㣬AC=1��
��AB=2��
�֡�D��AB���е㣬
��AD=1��$CD=\frac{1}{2}AB=1$��
�֡�EF�ǡ�ACD����λ�ߣ�
��$EF=DF=\frac{1}{2}$��
�ڡ�ACD�У�AD=CD����A=60�㣬
���ADC=60�㣬
�ڡ�FGD�У�GF=DF•sin60��=$\frac{{\sqrt{3}}}{4}$��
�����EFGH�����$S=EF•GF=\frac{1}{2}��\frac{{\sqrt{3}}}{4}=\frac{{\sqrt{3}}}{8}$��
��2����ͼ�ڣ�������ƶ��ľ���Ϊx����$0��x��\frac{1}{2}$��
���������CBD�ص�����Ϊ������ʱ��
��$0��x��\frac{1}{4}$��$S=\frac{1}{2}x•\sqrt{3}x=\frac{{\sqrt{3}}}{16}$��
��$x=\frac{{\sqrt{2}}}{4}��\frac{1}{4}$������ȥ����
���������CBD�ص�����Ϊֱ������ʱ����$\frac{1}{4}��x��\frac{1}{2}$��
�ص����ֵ����S=$\frac{{\sqrt{3}}}{4}x-\frac{1}{2}��\frac{1}{4}��\frac{{\sqrt{3}}}{4}=\frac{{\sqrt{3}}}{16}$��
��$x=\frac{3}{8}$��
�������ƶ��ľ���Ϊ$\frac{3}{8}$ʱ���������CBD�ص����ֵ������$\frac{{\sqrt{3}}}{16}$��
��3����ͼ�ۣ���H2Q��AB��Q��
��DQ=m����${H_2}Q=\sqrt{3}m$����$D{G_1}=\frac{1}{4}$��${H_2}{G_1}=\frac{1}{2}$��
��Rt��H2QG1��${��\sqrt{3}m��^2}+{��m+\frac{1}{4}��^2}={��\frac{1}{2}��^2}$��
��֮��$m=\frac{{-1��\sqrt{13}}}{16}$��������ȥ����
��$cos��=\frac{{Q{G_1}}}{{{H_2}{G_1}}}=\frac{{\frac{{-1+\sqrt{13}}}{16}+\frac{1}{4}}}{{\frac{1}{2}}}=\frac{{3+\sqrt{13}}}{8}$��
���� ������Ҫ������ֱ�������ε����ʣ���λ�ߵ����ʺ����Ǻ�������ȣ����÷������۵�˼�룬����ֱ���������ǽ�����Ĺؼ���

| �����ǹ� | �����ǹ� | �����ǹ� | |
| ���ۣ�Ԫ/ǧ�ˣ� | 15 | 25 | 30 |
| ǧ���� | 40 | 40 | 20 |
��2��Ϊ��ʹʲ���ǵĵ���ÿǧ�����ٽ���2Ԫ���̼Ҽƻ���ʲ�����м���ס��������ǹ���100ǧ�ˣ����������ɼ�������ǹ�����ǧ�ˣ�
| A�� | 360�� | B�� | 540�� | C�� | 720�� | D�� | 900�� |
| A�� | ��������ȵ�ʵ���� | B�� | ����������ȵ�ʵ���� | ||
| C�� | ֻ��һ��ʵ���� | D�� | û��ʵ���� |
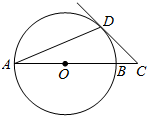 ��ͼ��AB�ǡ�O��ֱ������AB=2$\sqrt{2}$��AD���ң���DAB=22.5�㣬�ӳ�AB����C��ʹ�á�ACD=45�㣬��BC�ij��ǣ�������
��ͼ��AB�ǡ�O��ֱ������AB=2$\sqrt{2}$��AD���ң���DAB=22.5�㣬�ӳ�AB����C��ʹ�á�ACD=45�㣬��BC�ij��ǣ�������| A�� | 2$\sqrt{2}$-2 | B�� | $\sqrt{2}$ | C�� | 1 | D�� | 2-$\sqrt{2}$ |
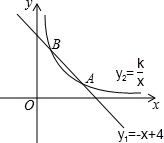 ��ͼ������y1=-x+4��ͼ���뺯��y2=$\frac{k}{x}$��x��0����ͼ����A��m��1����B��1��n�����㣮
��ͼ������y1=-x+4��ͼ���뺯��y2=$\frac{k}{x}$��x��0����ͼ����A��m��1����B��1��n�����㣮
 ��ͼ��һ������ɽ��A���½�Ϊ30���ɽ��AB����600m������һ������B������B��ɽ��BC����200m����ɽ��C������ɽ��C���۲����B�ĸ���Ϊ45�㣬��ɽ��CD=300+100$\sqrt{2}$m������ø��ű�ʾ����
��ͼ��һ������ɽ��A���½�Ϊ30���ɽ��AB����600m������һ������B������B��ɽ��BC����200m����ɽ��C������ɽ��C���۲����B�ĸ���Ϊ45�㣬��ɽ��CD=300+100$\sqrt{2}$m������ø��ű�ʾ����