题目内容
2．若函数y=-x+m2与y=4x-1的图象交于x轴，求m的值．分析 先根据y=4x-1求出与x轴的交点坐标，然后代入y=-x+m2求出m2，再根据平方根的定义求解．
解答 解：当y=0时，4x-1=0，
解得x=$\frac{1}{4}$，
∴两直线与x轴的交点是（$\frac{1}{4}$，0），
∴-$\frac{1}{4}$+m2=0，
解得m2=$\frac{1}{4}$，
∴m=±$\frac{1}{2}$．
点评 本题考查了两条直线的相交问题，先根据已知直线的解析式求出与x轴的交点是解题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
△ABC中，∠B，∠C的平分线交于F，∠ABC=42°，∠A=60°，求∠BFC的度数．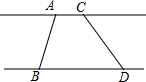
如图所示，直线a∥b且夹在两直线间的线段AB=CD，所以说夹在两平行线间的线段相等．这种说法对吗？请说明理由．
4．
如图，在直角三角形ABC中，∠ACB=90°，CA=4．点P是半圆弧AC的中点，连接BP，线段BP把图形APCB（指半圆和直角三角形ABC组成的图形）分成两部分，则这两部分面积之差的绝对值是（ ）
如图，在直角三角形ABC中，∠ACB=90°，CA=4．点P是半圆弧AC的中点，连接BP，线段BP把图形APCB（指半圆和直角三角形ABC组成的图形）分成两部分，则这两部分面积之差的绝对值是（ ）| A． | 2 | B． | 4 | C． | 1.5π-2 | D． | $\frac{2π}{3}$ |