题目内容
 如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )
如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:翻折变换(折叠问题)
专题:
分析:首先证明∠ACB=90°,然后借助三角形的面积公式列出关于线段CO的关系式问题即可解决.
解答: 解:由题意得:
解:由题意得:
AC=8,BC=6,AB=10,
CO⊥AB,CO=C′O;
∴AC2+BC2=AB2,
∴∠ACB=90°;
由三角形的面积公式得:
AC•BC=
AB•CO,
∴CO=
=
=4.8
∴CC′=
,
故选C.
 解:由题意得:
解:由题意得:AC=8,BC=6,AB=10,
CO⊥AB,CO=C′O;
∴AC2+BC2=AB2,
∴∠ACB=90°;
由三角形的面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
∴CO=
| AC•BC |
| AB |
| 48 |
| 10 |
∴CC′=
| 24 |
| 5 |
故选C.
点评:该命题以三角形为载体,以对称变换为方法,以考查全等三角形的性质、勾股定理的逆定理等几何知识点为核心构造而成;灵活运用有关定理来分析、判断、求解或证明是关键.

练习册系列答案
相关题目
 如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=( )
如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=( )| A、130° | B、140° |
| C、150° | D、160° |
下列各数-2,3,-(-0.75),-5.4,|-9|,-3,0,4中,属于整数的有m个,属于正数的有n个,则m,n的值为( )
| A、6,4 | B、5,5 |
| C、4,3 | D、3,6 |
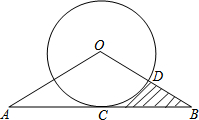 如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知OA=OB=6,∠A=30°.
如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知OA=OB=6,∠A=30°. 如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上的两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是
如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上的两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是