题目内容
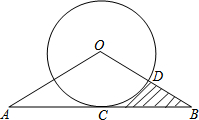 如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知OA=OB=6,∠A=30°.
如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知OA=OB=6,∠A=30°.(1)求⊙O的半径;
(2)求图中阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)首先连接OC,由线段AB与⊙O相切于点C,根据切线的性质,可得OC⊥AB,又由OA=OB=6,∠A=30°,即可求得⊙O的半径;
(2)首先求得扇形OCD与Rt△OBC的面积,继而求得答案.
(2)首先求得扇形OCD与Rt△OBC的面积,继而求得答案.
解答: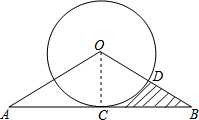 解:(1)连结OC,
解:(1)连结OC,
∵线段AB与⊙O相切于点C,
∴OC⊥AB,
∵OA=6,∠A=30°,
∴OC=3,
∴⊙O的半径为3.
(2)∵OA=OB,
∴∠A=∠B=30°,
∴∠COD=60°,
∴S扇形OCD=
=
π.
∴S阴影部分=S△OBC-S扇形OCD=
OC•BC-
π=
-
π.
 解:(1)连结OC,
解:(1)连结OC,∵线段AB与⊙O相切于点C,
∴OC⊥AB,
∵OA=6,∠A=30°,
∴OC=3,
∴⊙O的半径为3.
(2)∵OA=OB,
∴∠A=∠B=30°,
∴∠COD=60°,
∴S扇形OCD=
| 60×π×32 |
| 360 |
| 3 |
| 2 |
∴S阴影部分=S△OBC-S扇形OCD=
| 1 |
| 2 |
| 3 |
| 2 |
9
| ||
| 2 |
| 3 |
| 2 |
点评:此题考查了切线的性质、扇形的面积以及直角三角形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )
如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
在代数式
中,x的取值范围在数轴上可表示为( )
| x-1 |
A、 |
B、 |
C、 |
D、 |
 如图,共有线段,射线,直线各几条?其中能用字母表示的射线有几条?
如图,共有线段,射线,直线各几条?其中能用字母表示的射线有几条?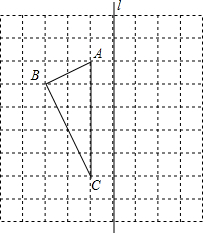 如图,正方形网格中每个小正方形边长都是1.
如图,正方形网格中每个小正方形边长都是1.