题目内容
在△ABC中,AB=AC=3,∠A=120°,求△ABC的外接圆的直径.
考点:三角形的外接圆与外心
专题:计算题
分析:作AD⊥BC于D,如图,根据等腰三角形的性质得BD=CD,∠BAD=∠CAD=
∠BAC=60°,即AD垂直平分BC,再根据垂径定理的推论得到△ABC的外接圆的圆心O在AD的延长线上,连结OB,接着证明△OAB为等边三角形,则OB=AB=3,由此可确定△ABC的外接圆的直径.
| 1 |
| 2 |
解答:解: 作AD⊥BC于D,如图,
作AD⊥BC于D,如图,
∵AB=AC=3,
∴BD=CD,∠BAD=∠CAD=
∠BAC=
×120°=60°,
∴AD垂直平分BC,
∴△ABC的外接圆的圆心O在AD的延长线上,
连结OB,
∵OA=OB,
∴△OAB为等边三角形,
∴OB=AB=3,
∴△ABC的外接圆的直径为6.
 作AD⊥BC于D,如图,
作AD⊥BC于D,如图,∵AB=AC=3,
∴BD=CD,∠BAD=∠CAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD垂直平分BC,
∴△ABC的外接圆的圆心O在AD的延长线上,
连结OB,
∵OA=OB,
∴△OAB为等边三角形,
∴OB=AB=3,
∴△ABC的外接圆的直径为6.
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
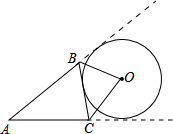 已知⊙O分别与△ABC的BC边,AB的延长线,AC的延长线相切,则∠BOC等于( )
已知⊙O分别与△ABC的BC边,AB的延长线,AC的延长线相切,则∠BOC等于( )A、
| ||
B、90°+
| ||
C、90°-
| ||
| D、180°-∠A |
 如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )
如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
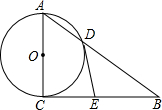 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,E为BC的中点,连接DE. 如图,共有线段,射线,直线各几条?其中能用字母表示的射线有几条?
如图,共有线段,射线,直线各几条?其中能用字母表示的射线有几条?