题目内容
 如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=( )
如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=( )| A、130° | B、140° |
| C、150° | D、160° |
考点:三角形内角和定理
专题:
分析:根据三角形的内角和定理可得∠ABC+∠ACB,再根据角平分线的定义求出∠ABD+∠ACE,再根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得解.
解答:解:∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
∵BD、CE是角平分线,
∴∠ABD+∠ACE=
(∠ABC+∠ACB)=
×140°=70°,
由三角形的外角性质得,∠BEC+∠BDC=∠ACE+∠A+∠ABD+∠A=70°+40°×2=150°.
故选C.
∴∠ABC+∠ACB=180°-40°=140°,
∵BD、CE是角平分线,
∴∠ABD+∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠BEC+∠BDC=∠ACE+∠A+∠ABD+∠A=70°+40°×2=150°.
故选C.
点评:本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
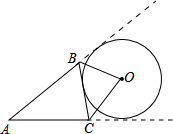 已知⊙O分别与△ABC的BC边,AB的延长线,AC的延长线相切,则∠BOC等于( )
已知⊙O分别与△ABC的BC边,AB的延长线,AC的延长线相切,则∠BOC等于( )A、
| ||
B、90°+
| ||
C、90°-
| ||
| D、180°-∠A |
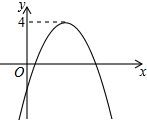 函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是( )
函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号的实数根 |
| C、有两个相等的实数根 |
| D、没有实数根 |
 如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )
如图,在△ABC中,AC=8,BC=6,AB=10,把△ABC沿AB边翻折成△ABC′,(在同一个平面内),则CC′的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列各组图形中,一定是全等图形的是( )
| A、两个周长相等的等腰三角形 |
| B、两个面积相等的长方形 |
| C、两个斜边相等的直角三角形 |
| D、两个直角边相等的等腰直角三角形 |
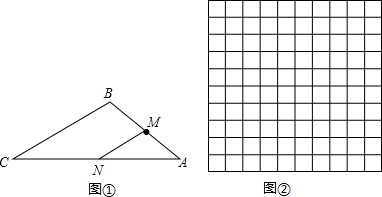
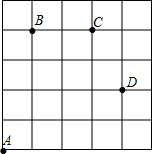 一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A、B、C、D都在格点上).规定:向上向右走为正,向下向左走为负.若从A到B记为:A→B(+1,+4),则从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A、B、C、D都在格点上).规定:向上向右走为正,向下向左走为负.若从A到B记为:A→B(+1,+4),则从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中