题目内容
3．已知不等式ax2+bx+c＞0的解是1＜x＜3，则a：b：c=1：（-8）：3．分析 根据题意可得方程ax2+bx+c=0的根是x1=1，x2=3且a＜0，再由根与系数的关系可用a表示出b、c的值，进而得出结论．
解答 解：∵不等式ax2+bx+c＞0的解是1＜x＜3，
∴方程ax2+bx+c=0的根是x1=1，x2=3且a＜0，
∴x1+x2=-$\frac{b}{2a}$=4，x1•x2=$\frac{c}{a}$=3，
∴b=-8a，c=3a，
∴a：b：c=1：（-8）：3．
故答案为：1：（-8）：3．
点评 本题考查的是二次函数与不等式组，根据题意得出一元二次方程的根是解答此题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
如图，在?ABCD中，AB=4cm，BC=7cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=3cm．
14．
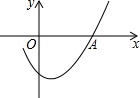如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x=1，下列结论正确的是（ ）
如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x=1，下列结论正确的是（ ）| A． | b2＜4ac | B． | ac＞0 | C． | 2a-b=0 | D． | a-b+c=0 |
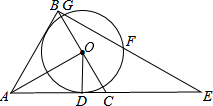如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC的延长线于点E，与⊙O相交于G、F两点．
15．下列几何体中，主视图、左视图、俯视图完全相同的是（ ）
| A． | 球 | B． | 圆锥 | C． | 圆柱 | D． | 长方体 |
