题目内容
17.在数-$\sqrt{2}$,0,1,$\sqrt{2}$中,最大的数是( )| A. | $\sqrt{2}$ | B. | 1 | C. | 0 | D. | $-\sqrt{2}$ |
分析 先将四个数分类,然后按照正数>0>负数的规则比较大小.
解答 解;将-$\sqrt{2}$,0,1,$\sqrt{2}$四个数分类可知1、$\sqrt{2}$为正数,-$\sqrt{2}$为负数,且$\sqrt{2}$>1,故最大的数为$\sqrt{2}$,
故选:A.
点评 此题主要考查了利用数轴比较实数的大小,解答此题的关键是熟知:数轴上的任意两个数,边的数总比左边的数大.

练习册系列答案
相关题目
7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
12.下列运算中,正确的是( )
| A. | $\sqrt{-2}$×$\sqrt{-3}$=$\sqrt{(-2)×(-3)}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$×3$\sqrt{2}$=6$\sqrt{6}$ | C. | $\sqrt{{a}^{2}-4}$=$\sqrt{{a}^{2}}$-$\sqrt{4}$=a-2 | D. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ |
9.在△ABC中,已知∠A=∠B=45°,BC=$\sqrt{2}$,则边AB的长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
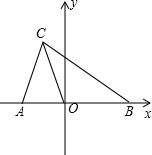 如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.
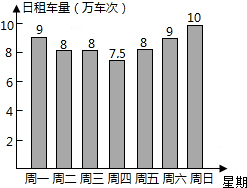 作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图:
作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图: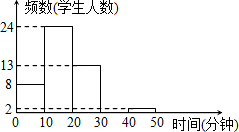 李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.
李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.