题目内容
初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
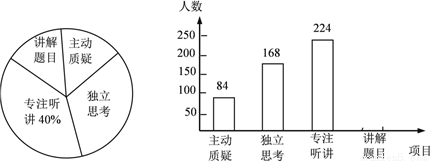
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
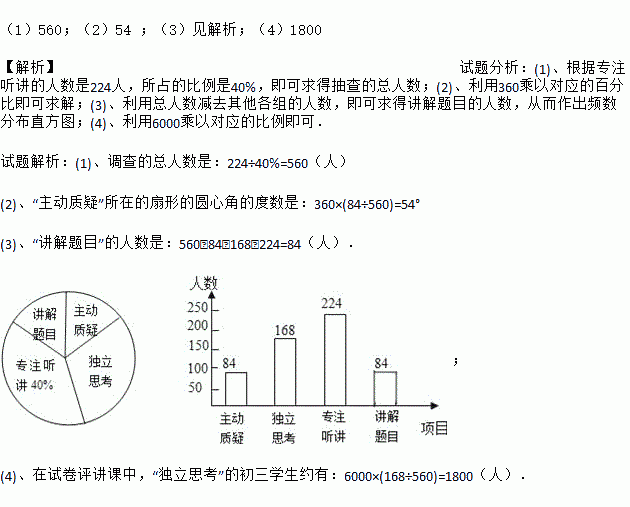
(1)560;(2)54 ;(3)见解析;(4)1800 【解析】试题分析:(1)、根据专注听讲的人数是224人,所占的比例是40%,即可求得抽查的总人数;(2)、利用360乘以对应的百分比即可求解;(3)、利用总人数减去其他各组的人数,即可求得讲解题目的人数,从而作出频数分布直方图;(4)、利用6000乘以对应的比例即可. 试题解析:(1)、调查的总人数是:224÷40%=560(人...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.
经过调查,得到如下数据:
销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
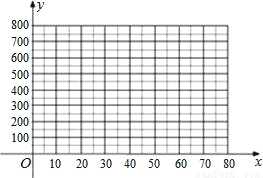
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系式,并求出函数关系式.
(2)物价部门规定,该工艺品的销售单价最高不超过45元/件,当销售单价x定为多少时,工艺厂试销该工艺品每天获得的利润8000元?(利润=销售总价﹣成本总价)
(3)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)

 -1时,代数式
-1时,代数式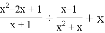 的值是 .
的值是 .
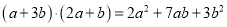 .
.
 B.
B.  C.
C.  D.
D.