题目内容
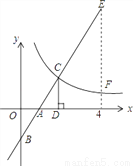
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.
练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
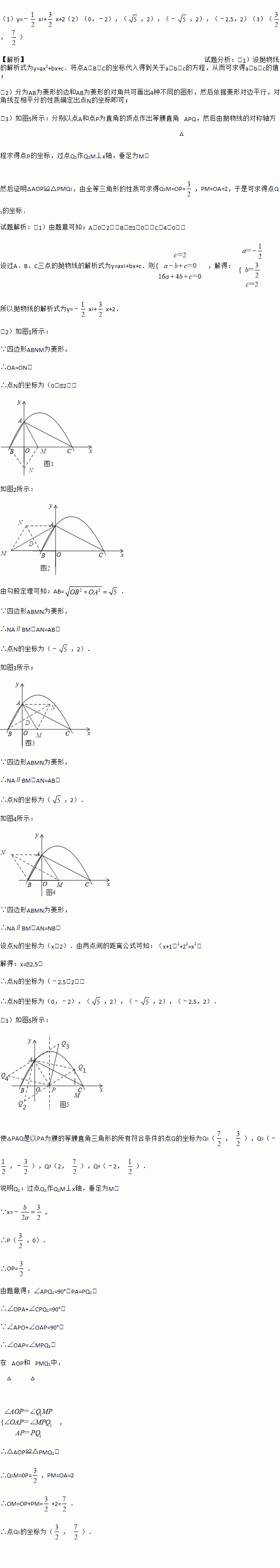

 .
.
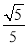 B.
B. 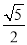 C.
C. 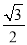 D.
D. 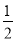
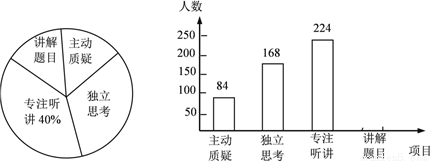
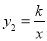 (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;