题目内容
10.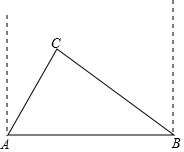 某县城在进行城市规划建设中,准备在相距1.6千米的两个超市A、B之间,扩建街道的宽度,但在A地的北偏东30°,B地的北偏西60°的C处有一半径为0.5千米的住宅小区,问在扩建公路时,这个小区是否有居民需要搬迁?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某县城在进行城市规划建设中,准备在相距1.6千米的两个超市A、B之间,扩建街道的宽度,但在A地的北偏东30°,B地的北偏西60°的C处有一半径为0.5千米的住宅小区,问在扩建公路时,这个小区是否有居民需要搬迁?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 根据题意,在△ABC中,∠ABC=30°,∠BAC=60°,AB=2千米,是否搬迁C点到AB的距离与0.5的大小关系,若距离大于0.5千米则不需搬迁,反之则需搬迁,因此求C点到AB的距离,作CD⊥AB于D点.
解答 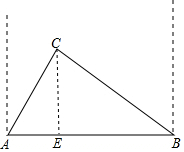 解:过C作CE⊥AB于E,
解:过C作CE⊥AB于E,
在Rt△ACE中,CE=tan60°•AE,
在Rt△CEB中,CE=tan30°•(1.6-AE)$\sqrt{3}$,
∴tan60°•AE=tan30°•(1.6-AE),
∴AE=0.4∴CE=0.4≈0.692>0.5
因此这个小区居民不需要搬迁.
点评 此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
2.估计$\frac{\sqrt{5}+1}{2}$介于( )之间.
| A. | 1.4与1.5 | B. | 1.5与1.6 | C. | 1.6与1.7 | D. | 1.7与1.8 |
14.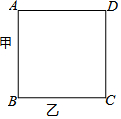 如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
 如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )| A. | AB边上 | B. | CA边上 | C. | DC边上 | D. | BD边上 |
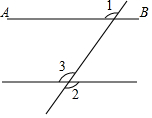 已知,如图,∠1=120°,∠2=120°,求证:AB∥CD.
已知,如图,∠1=120°,∠2=120°,求证:AB∥CD.