题目内容
15.二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0解为( )| A. | x1=-3 x2=-1 | B. | x1=1 x2=3 | C. | x1=-1 x2=3 | D. | x1=-3 x2=1 |
分析 首先求出二次函数图象与x轴的另一个交点坐标,进而求出方程ax2-2ax+c=0的解.
解答 解:∵y=ax2-2ax+c=a(x-1)2+c-a,
∴二次函数的图象的对称轴方程为直线x=1,
∵二次函数y=ax2-2ax+c的图象经过点(-1,0),
∴二次函数图象与x轴的另一个交点坐标为(3,0),
∴方程ax2-2ax+c=0解为x1=-1 x2=3,
故选C.
点评 本题主要考查了二次函数图象上点的坐标特征,解题的关键是求出二次函数图象与x轴的交点坐标,此题难度不大.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
5.腊月某一天的天气预报中,瑞安的最低温度是-2℃,哈尔滨的最低温度是-26℃,这一天瑞安的最低气温比哈尔滨的最低气温高( )
| A. | 24℃ | B. | -24℃ | C. | 28℃ | D. | -28℃ |
6.数:-$\frac{5}{11}$,0.123456…,0.$\stackrel{•}{2}$,0,$\sqrt{7}$,π,$\root{3}{27}$,5.121212中,无理数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.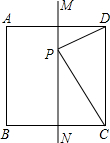 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
20.下列方程是一元二次方程的是( )
| A. | (x-1)(x+2)=x2+3 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}-2$=0 | C. | (x-1)2=2x-2 | D. | ax2+2x-1=0 |
7.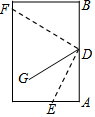 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).