题目内容
1.下列给出的方程:①(x+1)(x-1)-x2=0;②x2+1=0;③y2-2y-1=0;④x2-1=$\frac{1}{x}$.其中是一元二次方程的是( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ②③ |
分析 一元二次方程必须满足四个条件:(1)含有一个未知数;(2)未知数的最高次数是2;(3)二次项系数不为0;(4)是整式方程.
由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
解答 解:①由(x+1)(x-1)-x2=0得到:-1=0,不是方程,且不成立,故错误;
②x2+1=0;③y2-2y-1=0符合一元二次方程的定义,故正确;
④x2-1=$\frac{1}{x}$属于分式方程,故错误;
故选:D.
点评 本题考查了一元二次方程的定义.判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.这是一个需要识记的内容.

练习册系列答案
相关题目
9.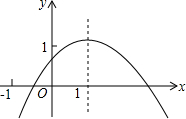 如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a-b>0,
③a+b+c>0,
④a-b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
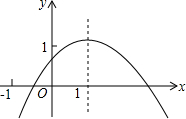 如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:①a<0,b<0,
②2a-b>0,
③a+b+c>0,
④a-b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ③④⑤ | D. | ①③④ |
16.用代数式表示a、b两数的和与a、b两数的差的积是( )
| A. | (a+b)(a-b) | B. | (a+b)•a-b | C. | a•(a+b)-b | D. | (a+b)-ab |
6.数:-$\frac{5}{11}$,0.123456…,0.$\stackrel{•}{2}$,0,$\sqrt{7}$,π,$\root{3}{27}$,5.121212中,无理数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.实数16的平方根是( )
| A. | 4 | B. | ±4 | C. | 2$\sqrt{2}$ | D. | ±2$\sqrt{2}$ |
10.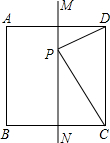 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
 如图,已知BD平分∠ABC,DE⊥AB于E,S=36cm2,AB=18cm,BC=12cm,则DE的长为$\frac{12}{5}$.
如图,已知BD平分∠ABC,DE⊥AB于E,S=36cm2,AB=18cm,BC=12cm,则DE的长为$\frac{12}{5}$.