题目内容
10．二次函数y=ax2的图象经过点（-1，-3），则二次函数y=ax2的解析式是y=-3x2．分析 直接把点（-1，-3）代入y=ax2中求出a的值即可．
解答 解：把点（-1，-3）代入y=ax2得a=-3，
所以二次函数解析式为y=-3x2．
故答案为y=-3x2．
点评 本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
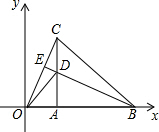如图，在平面直角坐标系中，等腰△OBC的边OB在x轴上，OB=CB，OB边上的高CA与OC边上的高BE相交于点D，连接OD，AB=$\sqrt{2}$，∠CBO=45°，在直线BE上求点M，使△BMC与△ODC相似，则点M的坐标是（1，$\sqrt{2}$-1）或（-$\sqrt{2}$，$\sqrt{2}$）．
5．抛物线y=-$\frac{1}{3}{x^2}$+3x-2与y=ax2+3x的形状相同，而开口方向相反，则a=（ ）
| A． | $-\frac{1}{3}$ | B． | 3 | C． | -3 | D． | $\frac{1}{3}$ |
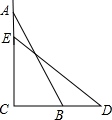如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.5米，求梯子顶端A下落了多少米？