题目内容
2.已知关于x的一元二次方程kx2-(2k-1)x+k=0有两个不相等的实根,求k的取值范围k<$\frac{1}{4}$且k≠0.分析 由条件可知该一元二次方程的判断式大于0,可得到一个关于k的不等式,可求出k的取值范围,需要验证k是否为0.
解答 解:该方程的判断式为:△=(2k-1)2-4k•k=-4k+1,
因为方程有两个不相等的实数根,所以△>0,
即-4k+1>0,解得k<$\frac{1}{4}$,
又因为该方程为一元二次方程,
所以k≠0,
所以k的取值范围为:k<$\frac{1}{4}$且k≠0.
故答案为:k<$\frac{1}{4}$且k≠0.
点评 本题主要考查一元二次方程根的判断式,掌握一元二次方程根的情况与判断式的关系是解题的关键,注意需要保证该方程为一元二次方程.

练习册系列答案
相关题目
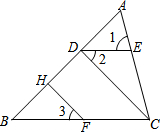 已知,如图,DE∥BC,∠A=60°,∠B=50°;
已知,如图,DE∥BC,∠A=60°,∠B=50°;