题目内容
15.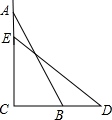 如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?
如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?
分析 在直角三角形ABC中,根据勾股定理得:AC=2米,由于梯子的长度不变,在直角三角形CDE中,根据勾股定理得CE=1.5米,所以AE=0.5米,即梯子的顶端下滑了0.5米.
解答 解:在Rt△ABC中,AB=2.5米,BC=1.5米,故AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2米,
在Rt△ECD中,AB=DE=2.5米,CD=(1.5+0.5)米,故EC=$\sqrt{D{E}^{2}-C{D}^{2}}$=$\sqrt{2.{5}^{2}-{2}^{2}}$=1.5米,
故AE=AC-CE=2-1.5=0.5米.
点评 本题主要考查了勾股定理的实际应用,此题中主要注意梯子的长度不变,分别运用勾股定理求得AC和CE的长,即可计算下滑的长度.

练习册系列答案
相关题目
3.若分式$\frac{{{x^2}-1}}{x+1}$的值为0,则x的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 2 |
20.已知一个平行四边形ABCD的周长是36,AB:AD=1:2,则AB的长是( )
| A. | 4 | B. | 16 | C. | 8 | D. | 6 |
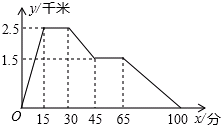 下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象回答下列问题:
下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象回答下列问题: (1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;
(1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;