题目内容
17．
如图，F是平行四边形ABCD的边CD上的点，FD=2FC，连结AF并延长交BC于E，CE=2，则AD的长为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 6 |
分析 根据平行四边形的性质得到AD∥BC，推出△ADF∽△CEF，根据平行四边形的性质得到$\frac{AD}{CE}=\frac{DF}{CF}$=2，即可得到结论．
解答 解：∵FD=2FC，
∴$\frac{DF}{CF}=2$，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴△ADF∽△CEF，
∴$\frac{AD}{CE}=\frac{DF}{CF}$=2，
∵CE=2，
∴AD=4．
故选C．
点评 此题主要考查了平行四边形的性质以及相似三角形的判定和性质，充分利用相似三角形对应边长成比例来求解．
练习册系列答案
相关题目
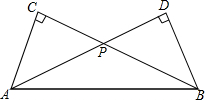如图，Rt△ABC中，∠ACB=90°，AC=4，BC=8，点P是BC边上的一个动点（不与B，C重合），过点B作射线AP的垂线，D为垂足，设CP=t．
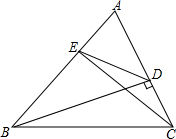如图，△ABC中，BD⊥AC，CE⊥AB，AD•AE=$\frac{1}{4}$AB•AC，求cosA的值．
如图，身高1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BA=4m，CA=0.8m，则树的高度为（ ）
已知：如图，直线AD与BC交于点O，OA=OD，OB=OC．求证：∠B=∠C．