题目内容
 如图,点P为正方形ABCD的边CD上一点,EF垂直平分BP分别交BC、AD于E、F,GP⊥EP交AD于G,连接BG交EF于H,下列结论:
如图,点P为正方形ABCD的边CD上一点,EF垂直平分BP分别交BC、AD于E、F,GP⊥EP交AD于G,连接BG交EF于H,下列结论:①BP=EF;②∠FHG=45°;③以BA为半径⊙B与GP相切;④若G为AD的中点,则DP=2CP,
其中正确的结论是( )
| A、①②③④ | B、①②③ |
| C、①②④ | D、①③④ |
考点:圆的综合题
专题:
分析:先作NF⊥BC于N,根据正方形的性质和垂直平分线的性质证明△BCP≌△FNE就可以得出BP=EF,作BM⊥PG于M,GP⊥EP,通过证明两次三角形全等就可以得出∠PBG=45°,从而求出∠FHG=45°,由切线的判定定理就可以求出以BA为半径⊙B与GP相切,当G为AD的中点时,设AG=GD=x,CP=y,则GM=x,PM=y,PD=2x-y,运用勾股定理就可以求出DP与CP的关系.
解答:解:(1)作NF⊥BC于N,
∴∠FNE=90°.
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠ADC=∠BAD=90°,AB=BC=CD=DA.
∴NF=AB,
∴NF=CB.
∵EF垂直平分BP,
∴∠2=∠3,∠2+∠NEF=90°.
∵∠1+∠NEF=90°,
∴∠1=∠2,
在△BCP和△FNE中,
,
∴△BCP≌△FNE,
∴BP=EF;故①正确;
作BM⊥PG于M,GP⊥EP,
∴BM∥EP,∠BMP=∠BMG=90°
∴∠3=∠5,∠BMP=∠C.
∴∠2=∠5
在△BPC和△BPM中
,
∴△BPC≌△BPM,
∴BC=AB=BM,
∴以BA为半径⊙B与GP相切.故③正确;
在Rt△BMG和Rt△BAG中,
,
∴Rt△BMG≌Rt△BAG,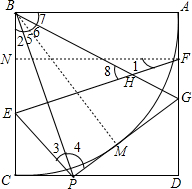
∴∠6=∠7.
∵∠2+∠5+∠6+∠7=90°,
∴2∠5+2∠6=90°,
∴∠5+∠6=45°
即∠PBG=45°.
∴∠8=45°.
∴∠FHG=45°故②正确;
当G为AD的中点时,设AG=GD=x,CP=y,则GM=x,PM=y,PD=2x-y,
在Rt△PGD中由勾股定理,得
(x+y)2=x2+(2x-y)2,
∴y=
x,
即CP=
x
∴PD=2x-
x=
x,
∴DP=2CP故④正确.
∴正确的有:①②③④.
故选A.
∴∠FNE=90°.
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠ADC=∠BAD=90°,AB=BC=CD=DA.
∴NF=AB,
∴NF=CB.
∵EF垂直平分BP,
∴∠2=∠3,∠2+∠NEF=90°.
∵∠1+∠NEF=90°,
∴∠1=∠2,
在△BCP和△FNE中,
|
∴△BCP≌△FNE,
∴BP=EF;故①正确;
作BM⊥PG于M,GP⊥EP,
∴BM∥EP,∠BMP=∠BMG=90°
∴∠3=∠5,∠BMP=∠C.
∴∠2=∠5
在△BPC和△BPM中
|
∴△BPC≌△BPM,
∴BC=AB=BM,
∴以BA为半径⊙B与GP相切.故③正确;
在Rt△BMG和Rt△BAG中,
|
∴Rt△BMG≌Rt△BAG,

∴∠6=∠7.
∵∠2+∠5+∠6+∠7=90°,
∴2∠5+2∠6=90°,
∴∠5+∠6=45°
即∠PBG=45°.
∴∠8=45°.
∴∠FHG=45°故②正确;
当G为AD的中点时,设AG=GD=x,CP=y,则GM=x,PM=y,PD=2x-y,
在Rt△PGD中由勾股定理,得
(x+y)2=x2+(2x-y)2,
∴y=
| 2 |
| 3 |
即CP=
| 2 |
| 3 |
∴PD=2x-
| 2 |
| 3 |
| 4 |
| 3 |
∴DP=2CP故④正确.
∴正确的有:①②③④.
故选A.
点评:本题是一道圆的综合试题考查了垂直平分线的性质,正方形的性质,全等三角形的判定及性质的而运用,圆的切线的判定方法的运用,勾股定理的性质的运用,在解答中运用作辅助线制造全等三角形是关键.

练习册系列答案
相关题目
已知:当x=1时,2ax2+bx的值为3,则当x=2时,ax2+bx的值为( )
| A、3 | B、6 | C、9 | D、12 |
 如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
用公式x=
解方程3x-1-2x2=0的过程中,a、b、c的值分别是( )
-b±
| ||
| 2a |
| A、a=3 b=-1 c=-2 |
| B、a=-2 b=-1 c=3 |
| C、a=-2 b=3 c=-1 |
| D、a=-1 b=3 c=-2 |
下列二次根式中不能再化简的二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式组
无解,则m的取值范围是( )
|
| A、m≥5 | B、m≥6 |
| C、m>6 | D、m≤6 |
 如图,△ABC中,AB=AC,∠BAC=70°,P为BC上一点,将△ABP绕点A按逆时针方向旋转到△ACP′位置,则∠AP′P的度数为( )
如图,△ABC中,AB=AC,∠BAC=70°,P为BC上一点,将△ABP绕点A按逆时针方向旋转到△ACP′位置,则∠AP′P的度数为( )| A、30° | B、60° |
| C、45° | D、55° |
 直线
直线 如图,⊙O中,弦AB垂直平分半径OC,垂足为P,若AB=6,则⊙O半径为
如图,⊙O中,弦AB垂直平分半径OC,垂足为P,若AB=6,则⊙O半径为