题目内容
3.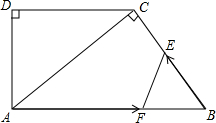 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出当t为何值时.四边形AFEC的面积为19.
分析 (1)根据平行线的性质得到∠BAC=∠DCA,根据相似三角形的判定定理证明即可;
(2)根据勾股定理求出AC,根据相似三角形的性质得到比例式,计算即可;
(3)过点E作AB的垂线,垂足为G,根据相似三角形的性质得到$\frac{EG}{AC}$=$\frac{BE}{AB}$,得到EF=$\frac{4}{5}$t,根据三角形的面积公式计算即可.
解答 解:(1)∵CD∥AB,
∴∠BAC=∠DCA,
∵AC⊥BC,∠ACB=90°,
∴∠D=∠ACB=90°,
∴△ACD∽△BAC;
(2)在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∵△ACD∽△BAC,
∴$\frac{DC}{AC}$=$\frac{AC}{AB}$,即$\frac{DC}{8}$=$\frac{8}{10}$,
解得:DC=6.4;
(3)过点E作AB的垂线,垂足为G,
则△ACB∽△EGB,
∴$\frac{EG}{AC}$=$\frac{BE}{AB}$,即$\frac{EG}{8}$=$\frac{t}{10}$,
解得,EF=$\frac{4}{5}$t,
则y=S△ABC-S△FBE=$\frac{1}{2}$×6×8-$\frac{1}{2}$×(10-2t)×$\frac{4}{5}$t=$\frac{4}{5}$t2-4t+24(0<t<5),
当y=19时,$\frac{4}{5}$t2-4t+24=19
解得t=$\frac{5}{2}$,
故当t=$\frac{5}{2}$时,y的值为19.
点评 本题考查的是相似三角形的判定和性质、二次函数的解析式的确定,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
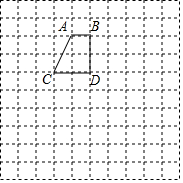 在如图中的正方形网格中有一个直角梯形ABCD,请你在图中分别按下列要求画出图形(不要求写出画法)
在如图中的正方形网格中有一个直角梯形ABCD,请你在图中分别按下列要求画出图形(不要求写出画法) 如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=78°,求∠DAC的度数.
如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=78°,求∠DAC的度数.