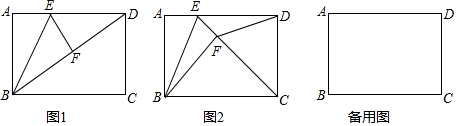
题目内容
14.如图1所示,已知在四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC,AE=DF,试说明BF=CE,当E,F相向运动时,形成图2、3、4、5、6图形,上述条件不变,BF和CE还相等吗?请证明你的结论.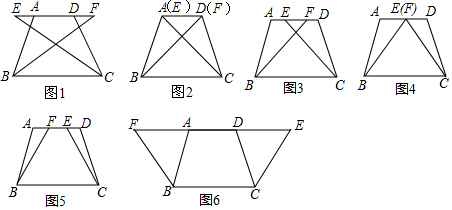
分析 根据两直线平行,同旁内角互补证明∠BAD=∠CDA,根据AE=DF证明AF=DE,再根据边角边定理证明△ABF和△DCE全等,根据全等三角形对应边相等即可证明BF=CE.利用边角边定理证明△ABC和△DCB全等,再根据全等三角形对应边相等即可证明.
解答 证明:∵AD∥BC,
∴∠BAD+∠ABC=180°,∠CDA+∠DCB=180°,
∵∠ABC=∠DCB,
∴∠BAD=∠CDA,
∵AE=DF,
∴AE+AD=DF+AD,
即AF=DE,
在△ABF和△DCE中,$\left\{\begin{array}{l}{AB=DC}\\{∠BAD=∠CDA}\\{AF=DE}\end{array}\right.$,
∴△ABF≌△DCE(SAS),
∴BF=CE;
相等.以图2为例,
在△ABC和△DCB中,$\left\{\begin{array}{l}{AB=DC}\\{∠ABC=∠DCB}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB(SAS),
∴BF=CE.
点评 本题考查边角边定理证明三角形全等和全等三角形对应边相等.此类题目,后一问根据前一问的解题思路求解是解题的捷径.

练习册系列答案
相关题目
8.为了让宜兴市的山更绿、水更清,2016年市委、市政府提出了确保到2018年实现全市绿化覆盖率达到43%的目标,已知2016年绿化覆盖率为40%,设从2016年起绿化覆盖率的年平均增长率为x,则可列方程( )
| A. | 40(1+2x)=43% | B. | 40(1+2x)=43 | C. | 40(1+x)2=43 | D. | 40(1+x)2=43% |
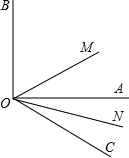 如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.
如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.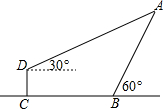 如图,一水库大坝AB的坡角为60°,在距离B点6米处有一平台CD,在D点测得点A的仰角为30°,已知点A,B,C,D在同一平面上,CD=2米,求这个大坝的高度.(结果保留很号)
如图,一水库大坝AB的坡角为60°,在距离B点6米处有一平台CD,在D点测得点A的仰角为30°,已知点A,B,C,D在同一平面上,CD=2米,求这个大坝的高度.(结果保留很号)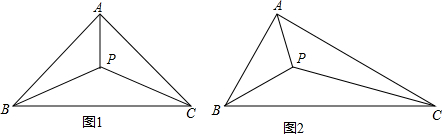
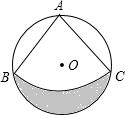 如图,⊙O直径为1米,在⊙O内有一个圆心角是90°的扇形ABC,且点A、B、C在⊙O上,计算弧AB的长及阴影面积.
如图,⊙O直径为1米,在⊙O内有一个圆心角是90°的扇形ABC,且点A、B、C在⊙O上,计算弧AB的长及阴影面积.