题目内容
19.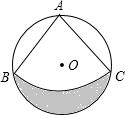 如图,⊙O直径为1米,在⊙O内有一个圆心角是90°的扇形ABC,且点A、B、C在⊙O上,计算弧AB的长及阴影面积.
如图,⊙O直径为1米,在⊙O内有一个圆心角是90°的扇形ABC,且点A、B、C在⊙O上,计算弧AB的长及阴影面积.
分析 连接OB、OC,根据圆周角定理得到∠BAC=90°,根据弧长公式求出弧AB的长;根据阴影部分的面积=半圆的面积-弓形的面积、利用扇形面积公式和三角形面积公式计算即可.
解答 解:连接OB、OC,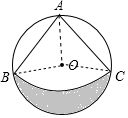
∵∠BAC=90°,
∴BC为⊙O的直径,
∴△ABC是等腰直角三角形,
∴AB=$\frac{\sqrt{2}}{2}$,∠AOB=90°,
∴弧AB的长为:$\frac{90π×1}{180}$=$\frac{π}{2}$米,
阴影部分的面积=半圆的面积-弓形的面积
=$\frac{1}{2}$×π×($\frac{1}{2}$)2-($\frac{90π×\frac{1}{2}}{360}$-$\frac{1}{2}$×1×$\frac{1}{2}$)
=$\frac{π}{8}$-$\frac{π}{8}$+$\frac{1}{4}$
=$\frac{1}{4}$米2.
点评 本题考查的是弧长的计算、扇形面积的计算,掌握弧长公式和扇形的面积公式是解题的关键.

练习册系列答案
相关题目
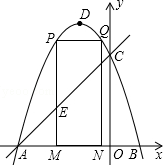 如图,抛物线y=-x2-2x+3 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
 如图,直线EF与AB相交于点G,与CD相交于点H,则∠AGH的对顶角是∠BGF;∠AGF与∠BGH是对顶角;∠AGH与∠AGF和∠BGH是邻补角;∠GHC的邻补角是∠GHD和∠CHE.
如图,直线EF与AB相交于点G,与CD相交于点H,则∠AGH的对顶角是∠BGF;∠AGF与∠BGH是对顶角;∠AGH与∠AGF和∠BGH是邻补角;∠GHC的邻补角是∠GHD和∠CHE.
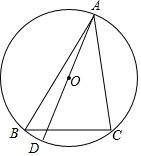 △ABC中,AB=8,BC=5,AC=7.圆O是△ABC的外接圆,AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.
△ABC中,AB=8,BC=5,AC=7.圆O是△ABC的外接圆,AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.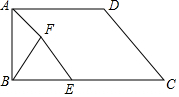 如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.
如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.