题目内容
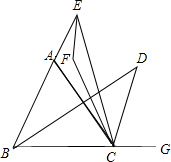 已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.
已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.考点:三角形内角和定理,三角形的外角性质
专题:
分析:易求∠F=180°-
∠A,易证∠A+2∠DBC=2∠D+2∠DBC,即可求得∠D=
∠A,即可解题.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠ACE、∠AEC的平分线相交于点F,∠ACE+∠AEC=∠A,
∴∠F=180°-
(∠ACE+∠AEC)=180°-
∠A,
∵∠ABC、∠ACG的平分线相交于点D,∠DCG=∠D+∠DBC,
∴2∠DCG=∠ACG=∠A+∠ABC=∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=
∠A,
∴∠F+∠D=180°.
∴∠F=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC、∠ACG的平分线相交于点D,∠DCG=∠D+∠DBC,
∴2∠DCG=∠ACG=∠A+∠ABC=∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=
| 1 |
| 2 |
∴∠F+∠D=180°.
点评:本题考查了三角形内角和为180°的性质,考查了角平分线平分角的性质,考查了三角形外角等于不相邻两内角和的性质,本题中分别用∠A表示∠F和∠D的值是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
设
的整数部分是m,
的整数部分是n,则(m+n)n的值是( )
| 2 |
| 8 |
| A、7 | B、8 | C、9 | D、10 |
若a=(
)-2,b=-|-
|,c=(-2)3,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、b<c<a |
| B、b<a<c |
| C、c<b<a |
| D、a<c<b |
 在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,AD=2,DC=11,求AB和BC的长.
在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,AD=2,DC=11,求AB和BC的长.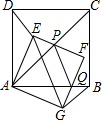 如图,正方形ABCD和正方形AGFE,连结DE、BG,且∠DAE<45°.
如图,正方形ABCD和正方形AGFE,连结DE、BG,且∠DAE<45°.
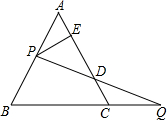 如图,边长为1的等边△ABC中,一动点P沿AB从A向B移动,动点Q以同样的速度从C出发沿BC的延长线运动,连PQ交AC边于D,作PE⊥AC于E,则DE的长为
如图,边长为1的等边△ABC中,一动点P沿AB从A向B移动,动点Q以同样的速度从C出发沿BC的延长线运动,连PQ交AC边于D,作PE⊥AC于E,则DE的长为