题目内容
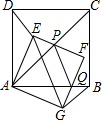 如图,正方形ABCD和正方形AGFE,连结DE、BG,且∠DAE<45°.
如图,正方形ABCD和正方形AGFE,连结DE、BG,且∠DAE<45°.(1)填空:∠DAB=∠EAG=
(2)连结AC、EG,AC交EF于P,AB交GF于Q,连结PQ.
①若PQ∥EG,求证:∠PAE=∠QAG;
②若正方形AGFE的边长为a,求△PFQ的周长(用含有a的代数式表示).
考点:四边形综合题
专题:
分析:(1)根据正方形各内角为90°即可解题;
(2)①易证EP=GQ,即可证明△EAP≌△GAQ,可得∠PAE=∠QAG,即可解题;
②易证∠BAG=∠DAE,即可证明△DAE≌△BAG,可得∠DAE=∠BAG,根据①中结论可得∠BAG=22.5°,即可求得FQ的值,易证△PFQ为等腰直角三角形,即可求得△PFQ的周长=(2+
)FQ,即可解题.
(2)①易证EP=GQ,即可证明△EAP≌△GAQ,可得∠PAE=∠QAG,即可解题;
②易证∠BAG=∠DAE,即可证明△DAE≌△BAG,可得∠DAE=∠BAG,根据①中结论可得∠BAG=22.5°,即可求得FQ的值,易证△PFQ为等腰直角三角形,即可求得△PFQ的周长=(2+
| 2 |
解答:解:(1)∵四边形ABCD和四边形AGFE均为正方形,
∴∠DAB=∠EAG=90°,
故答案为 90°;
(2)①∵PQ∥EG,
∴
=
,
∵EF=FG,
∴EP=GQ,
在△EAP和△GAQ中,
,
∴△EAP≌△GAQ,
∴∠PAE=∠QAG;
②∵∠DAE+∠EAB=90°,∠BAG+∠EAB=90°,
∴∠BAG=∠DAE,
在△DAE和△BAG中,
,
∴△DAE≌△BAG(SAS),
∴∠DAE=∠BAG,
∵∠PAE=∠QAG,
∴∠DAE=∠PAE,
∵∠DAE+∠PAE=∠DAC=45°,
∴∠BAG=22.5°,
∴GQ=AG•tan22.5°=(
-1)a,
∴FQ=a-(
-1)a=(2-
)a,
∵PQ∥EG,
∴△PFQ为等腰直角三角形,
∴PQ=
FQ,PF=FQ,
∴△PFQ的周长=FQ+PF+PQ=(2+
)FQ=(2+
)(2-
)a=2a.
∴∠DAB=∠EAG=90°,
故答案为 90°;
(2)①∵PQ∥EG,
∴
| GQ |
| FG |
| EP |
| EF |
∵EF=FG,
∴EP=GQ,
在△EAP和△GAQ中,
|
∴△EAP≌△GAQ,
∴∠PAE=∠QAG;
②∵∠DAE+∠EAB=90°,∠BAG+∠EAB=90°,
∴∠BAG=∠DAE,
在△DAE和△BAG中,
|
∴△DAE≌△BAG(SAS),
∴∠DAE=∠BAG,
∵∠PAE=∠QAG,
∴∠DAE=∠PAE,
∵∠DAE+∠PAE=∠DAC=45°,
∴∠BAG=22.5°,
∴GQ=AG•tan22.5°=(
| 2 |
∴FQ=a-(
| 2 |
| 2 |
∵PQ∥EG,
∴△PFQ为等腰直角三角形,
∴PQ=
| 2 |
∴△PFQ的周长=FQ+PF+PQ=(2+
| 2 |
| 2 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了特殊角的三角函数值,考查了正方形的性质,本题中求证△DAE≌△BAG是解题的关键.

练习册系列答案
相关题目
 美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )
美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )| A、2009年该区的绿地面积为420公顷 |
| B、2011年的绿地面积增长最快 |
| C、从2009年到2012年,每年绿地面积的增长率都在增长 |
| D、从2009年到2012年,每年的绿地面积都在增长 |
 如图是一个照相机成像的示意图,如果底片XY宽35mm,焦距是50mm,能拍摄5m外的景物有多宽?如果焦距是70mm呢?
如图是一个照相机成像的示意图,如果底片XY宽35mm,焦距是50mm,能拍摄5m外的景物有多宽?如果焦距是70mm呢?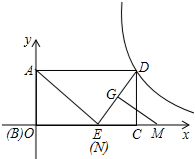 如图,在平面直角坐标系中,已知矩形ABCD,E是BC上一点,∠AED=90°,AB=6,SIN∠AEB=
如图,在平面直角坐标系中,已知矩形ABCD,E是BC上一点,∠AED=90°,AB=6,SIN∠AEB=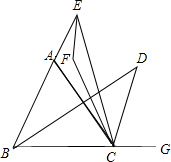 已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.
已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为