题目内容
 在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,AD=2,DC=11,求AB和BC的长.
在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,AD=2,DC=11,求AB和BC的长.考点:勾股定理,含30度角的直角三角形
专题:
分析:先根据四边形内角和定理求出∠B的度数,再延长AD交BC的延长线于点H,故可得出∠H=30°,由此可得出DH与CH的长,再由相似三角形的判定定理可得出△HDC∽△HBA,再根据相似三角形的对应边成比例即可得出结论.
解答: 解:∵在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,
解:∵在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,
∴∠B=180°-120°=60°.
延长AD交BC的延长线于点H,
在△ABH中,
∵∠A=90°,∠B=60°,
∴∠H=30°.
∵∠C=90°,DC=11,
∴DH=2CD=22,
∴CH=
=
=11
.
∵∠H=∠H,∠A=∠DCH=90°,
∴△HDC∽△HBA,
∴
=
=
,即
=
=
,解得AB=8
,BC=5
.
 解:∵在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,
解:∵在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,∴∠B=180°-120°=60°.
延长AD交BC的延长线于点H,
在△ABH中,
∵∠A=90°,∠B=60°,
∴∠H=30°.
∵∠C=90°,DC=11,
∴DH=2CD=22,
∴CH=
| DH2-CD2 |
| 222-112 |
| 3 |
∵∠H=∠H,∠A=∠DCH=90°,
∴△HDC∽△HBA,
∴
| CD |
| AB |
| CH |
| AD+DH |
| DH |
| BC+CH |
| 11 |
| AB |
11
| ||
| 2+22 |
| 22 | ||
BC+11
|
| 3 |
| 3 |
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一个照相机成像的示意图,如果底片XY宽35mm,焦距是50mm,能拍摄5m外的景物有多宽?如果焦距是70mm呢?
如图是一个照相机成像的示意图,如果底片XY宽35mm,焦距是50mm,能拍摄5m外的景物有多宽?如果焦距是70mm呢?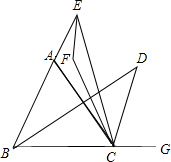 已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.
已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.