题目内容
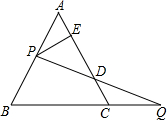 如图,边长为1的等边△ABC中,一动点P沿AB从A向B移动,动点Q以同样的速度从C出发沿BC的延长线运动,连PQ交AC边于D,作PE⊥AC于E,则DE的长为
如图,边长为1的等边△ABC中,一动点P沿AB从A向B移动,动点Q以同样的速度从C出发沿BC的延长线运动,连PQ交AC边于D,作PE⊥AC于E,则DE的长为考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:作PF∥BC,易证△APF为等边三角形,可得AE=EF,易证∠Q=∠DPF,即可证明△DPE≌△DQC,可得CD=DF,即可求得DE=
AC,即可解题.
| 1 |
| 2 |
解答:解:作PF∥BC,

∵PF∥BC,
∴△APF为等边三角形,∠Q=∠DPF,
∴PF=AP,∴PF=CQ,
∵PE⊥AD,
∴AE=EF,
在△DPE和△DQC中,
,
∴△DPE≌△DQC(AAS)
∴CD=DF,
∴DE=DF+EF=AE+CD=
AC=
,
故答案为
.

∵PF∥BC,
∴△APF为等边三角形,∠Q=∠DPF,
∴PF=AP,∴PF=CQ,
∵PE⊥AD,
∴AE=EF,
在△DPE和△DQC中,
|
∴△DPE≌△DQC(AAS)
∴CD=DF,
∴DE=DF+EF=AE+CD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了等边三角形三线合一的性质,本题中求证△DPE≌△DQC是解题的关键.

练习册系列答案
相关题目
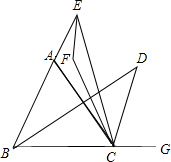 已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.
已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为