题目内容
1.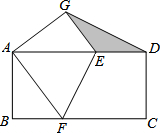 如图:矩形ABCD中,AB=4,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,
如图:矩形ABCD中,AB=4,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,(1)求证:△BAF≌△GAE
(2)求图中阴影部分的面积.
分析 (1)利用ASA证明两个三角形全等;
(2)首先利用勾股定理求出AF的长,进而求出AE的长,利用三角形的面积公式求出阴影部分面积.
解答 解:(1)∵∠BAF+∠FAE=∠FAE+∠EAG=90°,
∴∠BAF=∠EAG,
∵∠B=∠AGE=90°,AB=AG,
∴△BAF≌△GAE,
(2)由题意知,AF=FC,AB=CD=AG=4,BC=AD=8
在Rt△ABF中,由勾股定理知AB2+BF2=AF2,即42+(8-AF)2=AF2,
解得:AF=5,
∵△BAF≌△GAE,
∴AE=AF=5,ED=GE=3,
∵S△GAE=$\frac{1}{2}$AG•GE=$\frac{1}{2}$AE•AE边上的高,
∴AE边上的高=$\frac{12}{5}$,
∴S△GED=$\frac{1}{2}$ED•AE边上的高=$\frac{1}{2}$×3×$\frac{12}{5}$=$\frac{18}{5}$.
点评 本题利用了矩形的性质和翻折的性质、勾股定理、全等三角形的判定和性质求解,注意翻折前后对应边相等,难度一般.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
6.下列图形属于平移位置变换的是( )
| A. |  | B. |  | C. |  | D. |  |
13.下列说法不正确的是( )
| A. | 平行四边形的对边平行且相等 | B. | 平行四边形对角线互相平分 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
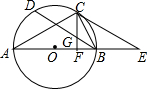 如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.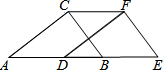 如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.