题目内容
1.在△ABC中,∠C=90°,AC=0.9cm,BC=1.2cm,则斜边上的高CD=0.72.分析 根据勾股定理求出AB的长,利用直角三角形的面积的两种求法即可列出方程求出CD边上的高.
解答 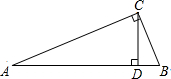 解:∵在△ABC中,∠C=90°,AC=0.9cm,BC=1.2cm,
解:∵在△ABC中,∠C=90°,AC=0.9cm,BC=1.2cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{0.{9}^{2}+1.{2}^{2}}$=1.5.
又∵$\frac{1}{2}$BC•AC=$\frac{1}{2}$AB•CD,
∴1.2×0.9=1.5CD,
∴CD=0.72.
故答案为0.72.
点评 本题考查了勾股定理和直角三角形面积的求法,知道三角形的面积公式是解题的关键.

练习册系列答案
相关题目
11.已知数轴上的两点A、B分别表示有理数a,-1,那么A、B两点之间的距离是( )
| A. | a-(-1) | B. | |a-1| | C. | |a+1| | D. | |a|+|-1| |
12.某作物原产量为n kg,增产30%后的产量为( )
| A. | 30%n kg | B. | (1-30%)n kg | C. | (1+30%)n kg | D. | (n+30%)n kg |
9.Rt△ABC中,∠C=90°,AC=5,BC=12,则连接两条直角边中点的线段长为( )
| A. | 13 | B. | 6.5 | C. | 7 | D. | 8 |
16.已知x-2y=3,则7-2x+4y的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.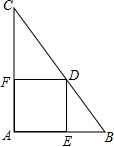 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{11}{2}$ |
10.若实数x,y满足(x2+y2)2+2(x2+y2)=0,则x2+y2的值为( )
| A. | 0 | B. | -2 | C. | 0或-2 | D. | 0或2 |