题目内容
9．Rt△ABC中，∠C=90°，AC=5，BC=12，则连接两条直角边中点的线段长为（ ）| A． | 13 | B． | 6.5 | C． | 7 | D． | 8 |
分析 首先利用勾股定理求出斜边AB的长，再根据三角形中位线定理即可求出连结两条直角边中点的线段长．
解答 解：∵∠C=90°，AC=5，BC=12，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13，
∴两条直角边中点的线段长=$\frac{1}{2}$AB=6.5，
故选B．
点评 此题考查的是勾股定理的运用以及三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
19．下列计算正确的是（ ）
| A． | -6+（-3）+（-2）=-1 | B． | 7+（-0.5）+2-3=5.5 | C． | -3-3=0 | D． | $（{-1}）-（{-\frac{3}{4}}）+（-4）=3\frac{3}{4}$ |
20．单项式-3mx3y的次数为（ ）
| A． | 3 | B． | 4 | C． | 3+m | D． | 4+m |
17．多项式axy2-$\frac{1}{3}$x与bxy2+$\frac{3}{4}$x的和是一个单项式，则a，b的关系是 （ ）
| A． | a=-b | B． | a=b=0 | C． | a=b | D． | 不能确定 |
如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDE，请你添加一个条件，使DE=DF，你添加的条件是∠B=∠C或∠BED=∠CFD（不再添加辅助线和字母）
18．下列等式或说法一定正确的是（ ）
| A． | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$ | B． | $\sqrt{{a}^{2}-{b}^{2}}$不是最简根式 | ||
| C． | 若a＜0，则$\sqrt{{a}^{4}}$=a2 | D． | $\sqrt{18}$或$\sqrt{48}$是同类二次根式 |
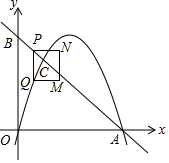如图，在平面直角坐标系中，点A，B分别在x轴，y轴的正半轴上，OA=OB=4，经过点O、A的抛物线y=ax2+bx交AB于点C，点C的横坐标为1，点P在线段AB上，当点P与点A，C均不重合时，过点P与x轴垂直的直线交此抛物线于点Q，以PQ为边向右作矩形PQMN，且PN=1，设点P的横坐标为m．