题目内容
11.已知x+y=5,xy=$\frac{9}{4}$,则x2y+xy2=$\frac{45}{4}$,x-y=4.分析 根据提公因式法,可分解因式,根据代数式求值,可得答案.
解答 解:x2y+xy2=xy(x+y),
当x+y=5,xy=时,原式=$\frac{9}{4}$×5=$\frac{45}{4}$,
x-y=$\sqrt{(x+y)^{2}-4xy}$=$\sqrt{{5}^{2}-4×\frac{9}{4}}$=4,
故答案为:$\frac{45}{4}$,4.
点评 本题考查了因式分解,利用完全平方公式是解题关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.在$-1\frac{1}{2}$,1.2,-2,0,-(-2)中,非负数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.一个正方形的面积为2,则其边长可估算为( )
| A. | 1.2与1.3之间 | B. | 1.3与1.4之间 | C. | 1.4与1.5之间 | D. | 1.5与1.6之间 |
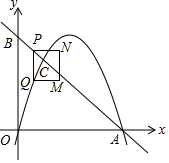 如图,在平面直角坐标系中,点A,B分别在x轴,y轴的正半轴上,OA=OB=4,经过点O、A的抛物线y=ax2+bx交AB于点C,点C的横坐标为1,点P在线段AB上,当点P与点A,C均不重合时,过点P与x轴垂直的直线交此抛物线于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m.
如图,在平面直角坐标系中,点A,B分别在x轴,y轴的正半轴上,OA=OB=4,经过点O、A的抛物线y=ax2+bx交AB于点C,点C的横坐标为1,点P在线段AB上,当点P与点A,C均不重合时,过点P与x轴垂直的直线交此抛物线于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m. 如图,5×5的正方形网络中,以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出4个,在5×5的正方形网络中一共可以作出95个与△ABC全等的三角形.(△ABC本身除外)
如图,5×5的正方形网络中,以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出4个,在5×5的正方形网络中一共可以作出95个与△ABC全等的三角形.(△ABC本身除外)