题目内容
18.若x=$\frac{2}{\sqrt{3}-1}$,$\frac{1}{y}$=(1-$\frac{\sqrt{3}}{2}$)(x+1)-$\frac{\sqrt{3}}{4}$,则y=8+4$\sqrt{3}$.分析 先化简x,得出x=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1,再将x=$\sqrt{3}$+1代入$\frac{1}{y}$,进而求出y即可.
解答 解:∵x=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1,
∴$\frac{1}{y}$=(1-$\frac{\sqrt{3}}{2}$)(x+1)-$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$(2-$\sqrt{3}$)($\sqrt{3}$+2)-$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$(4-3)-$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$
=$\frac{2-\sqrt{3}}{4}$,
∴y=$\frac{4}{2-\sqrt{3}}$=$\frac{4(2+\sqrt{3})}{(2-\sqrt{3})(2+\sqrt{3})}$=8+4$\sqrt{3}$.
故答案为8+4$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,利用了平方差公式,注意:二次根式的运算结果要化为最简二次根式.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
7.下列实数中,无理数是( )
| A. | $\sqrt{16}$ | B. | 3.14159 | C. | 0 | D. | -$\sqrt{12}$ |
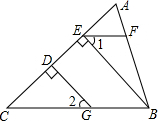 如图所示,已知AB⊥BC,GD⊥AC于点D,BE⊥AC于点E,∠1=∠2,判断EF与AB的位置关系,并说明理由.
如图所示,已知AB⊥BC,GD⊥AC于点D,BE⊥AC于点E,∠1=∠2,判断EF与AB的位置关系,并说明理由.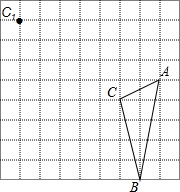 在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,
在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,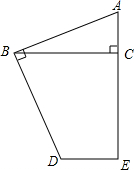 如图,∠ABD=90°,AB=BD,∠ACB=90°,∠CED=90°,BC=10cm.线段BC⊥AE,求四边形ABDE的面积.
如图,∠ABD=90°,AB=BD,∠ACB=90°,∠CED=90°,BC=10cm.线段BC⊥AE,求四边形ABDE的面积.