题目内容
5．如果一组数据x1、x2、x3、x4的平均数为$\overline{x}$，那么另一组数x1、x2+1、x3+2、x4+3的平均数为（ ）| A． | $\overline{x}$ | B． | $\overline{x}$+1 | C． | $\overline{x}$+1.5 | D． | $\overline{x}$+6 |
分析 根据平均数的性质知先求出x1+x2+x3+x4，再求出x1、x2+1、x3+2、x4+3的平均数即可．
解答 解：∵数据x1、x2、x3、x4的平均数为$\overline{x}$，
∴数据x1+x2+x3+x4=4$\overline{x}$，
∴数x1、x2+1、x3+2、x4+3的平均数为：
（x1+x2+1+x3+2+x4+3）÷4
=（4$\overline{x}$+6）÷4
=$\overline{x}$+1.5．
故选C．
点评 本题考查的是样本平均数的求法．解决本题的关键是用一组数据的平均数表示另一组数据的平均数．
练习册系列答案
相关题目
15．
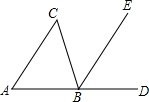如图，点D是△ABC的边AB延长线上一点，BE∥AC，若∠C=50°，∠DBE=60°，则∠DBC的度数为（ ）
如图，点D是△ABC的边AB延长线上一点，BE∥AC，若∠C=50°，∠DBE=60°，则∠DBC的度数为（ ）| A． | 70° | B． | 100° | C． | 110° | D． | 120° |
16．
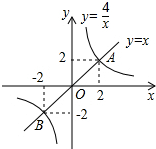正比例函数y=x与反比例函数y=$\frac{4}{x}$的图象交于A（2，2）、B（-2，-2）两点，当x＞$\frac{4}{x}$时，x的取值范围是（ ）
正比例函数y=x与反比例函数y=$\frac{4}{x}$的图象交于A（2，2）、B（-2，-2）两点，当x＞$\frac{4}{x}$时，x的取值范围是（ ）| A． | -2＜x＜0或x＞2 | B． | -2＜x＜0或0＜x＜2 | C． | x＞2 | D． | x＜-2 |
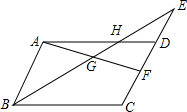如图，在?ABCD中，DH=$\frac{1}{2}$AH，点F是边CD的中点，
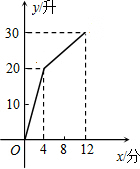有一进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量是两个常数，容器内的水量y（单位：L）与时间x（单位：分）之间的关系如图所示：
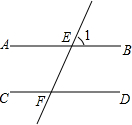已知，直线AB、CD被EF所截，∠AEF=∠EFD，求证：AB∥CD．