题目内容
14.有一个一次函数的图象,小可和小遥分别说出了它的两个特征:小可:图象与x轴交于点(6,0);
小遥:图象与x轴、y轴围成的三角形的面积是9.
你知道这个一次函数的解析式吗.
分析 根据一次函数的图象与x轴交于点(6,0),且与x轴、y轴围成的三角形的面积是9,用待定系数法可求出函数关系式.
解答 解:设一次函数的关系式为y=kx+b(k≠0),
∵图象与x轴交于点(6,0),即6k+b=0,k=-$\frac{b}{6}$,
又∵图象与x轴、y轴围成的三角形的面积是9,即$\frac{1}{2}$×6×|b|=9,b=±3,
当b=3时,k=-$\frac{3}{6}$=-$\frac{1}{2}$,函数关系式为y=-$\frac{1}{2}$x+3;
当b=-3时,k=$\frac{3}{6}$=$\frac{1}{2}$,函数关系式为y=$\frac{1}{2}$x-3;
故所求函数的关系式为y=-$\frac{1}{2}$x+3或y=$\frac{1}{2}$x-3.
点评 本题考查了待定系数法求一次函数的解析式,要注意利用一次函数的特点,列出方程,求出未知数的值,即可求得函数的解析式.

练习册系列答案
相关题目
5.如果一组数据x1、x2、x3、x4的平均数为$\overline{x}$,那么另一组数x1、x2+1、x3+2、x4+3的平均数为( )
| A. | $\overline{x}$ | B. | $\overline{x}$+1 | C. | $\overline{x}$+1.5 | D. | $\overline{x}$+6 |
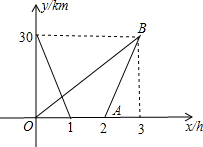 小强开车、小斌骑自行车分别同时从各自的家中出发,匀速相向而行,小强在到达小斌家后停留1h,原路返回自己家,小斌一直匀速骑电动车3h后,与小强同时到达小强家,如图表示两人距小斌家的距离y(km)与时间x(h)之间的函数关系
小强开车、小斌骑自行车分别同时从各自的家中出发,匀速相向而行,小强在到达小斌家后停留1h,原路返回自己家,小斌一直匀速骑电动车3h后,与小强同时到达小强家,如图表示两人距小斌家的距离y(km)与时间x(h)之间的函数关系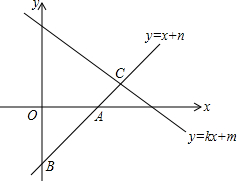 如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论:
如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论: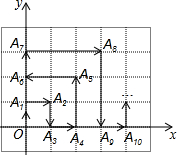 如图,在一单位为1的方格纸上建立直角坐标系,动点P按图中箭头所示方向运动,第一次从原点运动到点A1(0,1),第二次运动到点A2(1,1),第三次接着运动到点A3(1,0),…,按这样的运动规律,经过第2014次运动后,动点P运动到的点A2014的坐标是(672,0).
如图,在一单位为1的方格纸上建立直角坐标系,动点P按图中箭头所示方向运动,第一次从原点运动到点A1(0,1),第二次运动到点A2(1,1),第三次接着运动到点A3(1,0),…,按这样的运动规律,经过第2014次运动后,动点P运动到的点A2014的坐标是(672,0).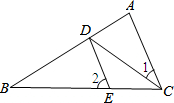 如图,已知CD平分∠ACB,DE∥AC,∠1=40°,则∠2=80°.
如图,已知CD平分∠ACB,DE∥AC,∠1=40°,则∠2=80°.