题目内容
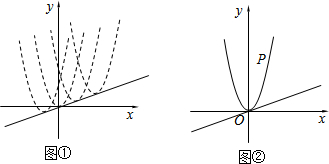
17.数学活动课上,小君在平面直角坐标系中对二次函数图象的平移进行了研究.图①是二次函数y=(x-a)2+$\frac{a}{3}$(a为常数)当a=-1、0、1、2时的图象.当a取不同值时,其图象构成一个“抛物线簇”.小君发现这些二次函数图象的顶点竟然在同一条直线上!
(1)小君在图①中发现的“抛物线簇”的顶点所在直线的函数表达式为y=$\frac{1}{3}$x;
(2)如图②,当a=0时,二次函数图象上有一点P(2,4).将此二次函数图象沿着(1)中发现的直线平移,记二次函数图象的顶点O与点P的对应点分别为O1、P1.若点P1到x轴的距离为5,求平移后二次函数图象所对应的函数表达式.
分析 (1)根据题意得出抛物线的顶点坐标,根据待定系数法即可求得;
(2)根据平移的规律得出点O1的坐标为 ( 3,1)或 (-27,-9),从而求得解析式.
解答 解:(1)∵当a=-1时,抛物线的顶点为(-1,-$\frac{1}{3}$),当a=0时,抛物线的顶点为(0,0),
∴设直线为y=kx,
代入(-1,-$\frac{1}{3}$)得,-$\frac{1}{3}$=-k,
解得k=$\frac{1}{3}$,
∴“抛物线簇”的顶点所在直线的函数表达式为y=$\frac{1}{3}$x,
故答案为y=$\frac{1}{3}$x.
(2)由题意得:点P1的纵坐标为5或-5,
∴抛物线沿着直线向上平移了1个单位或向下平移了9个单位,
∴此时点O1的纵坐标为1或-9,
代入直线y=$\frac{1}{3}$x求得横坐标为3或-27,
∴点O1的坐标为 ( 3,1)或 (-27,-9),
∴平移后的二次函数的表达式为y=(x-3)2+1或y=(x+27)2-9.
点评 本题考查了待定系数法求一次函数的解析式,二次函数的图象与几何变换,求得平移后O1的顶点坐标是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
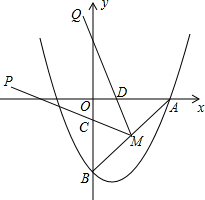 如图,抛物线y=ax2-2ax-4交x轴的正半轴于点A,交y轴于点B,且OA=OB.
如图,抛物线y=ax2-2ax-4交x轴的正半轴于点A,交y轴于点B,且OA=OB.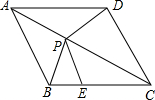 如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.
如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.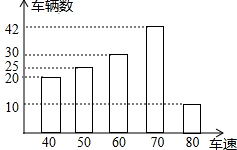 为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是70千米/时.
为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是70千米/时. 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系.