题目内容
8.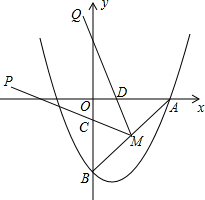 如图,抛物线y=ax2-2ax-4交x轴的正半轴于点A,交y轴于点B,且OA=OB.
如图,抛物线y=ax2-2ax-4交x轴的正半轴于点A,交y轴于点B,且OA=OB.(1)求该抛物线的解析式;
(2)若点M为AB的中点,且∠PMQ=45°,∠PMQ在AB的同侧,以点M为旋转中心将∠PMQ旋转,MP交y轴于点C,MQ交x轴于点D.设AD=m(m>0),BC=n,求n与m之间的函数关系式;
(3)在(2)的条件下,当∠PMQ的一边恰好经过该抛物线与x轴的另一个交点时,直接写出∠PMQ的另一边与x轴的交点坐标.
分析 (1)根据抛物线的解析式可得到点B的坐标,根据条件可求出点A的坐标,然后运用待定系数法就可解决问题;
(2)易得△AOB是等腰直角三角形,从而可得∠OAB=∠OBA=45°,AB=4$\sqrt{2}$,即可得到AM=BM=2$\sqrt{2}$,结合条件∠CMD=45°可推出△ADM∽△BMC,然后运用相似三角形的性质就可解决问题;
(3)设抛物线y=$\frac{1}{2}$x2-x-4与x轴另一个交点为E,只需令y=0,即可得到点E的坐标,根据中点坐标公式可求出点M的坐标.①当MP经过点E时,运用待定系数法可求出直线PM的解析式,即可得到点C的坐标,从而可求出n的值,再利用n与m的关系可求出m,就可求出点D的坐标;②当MQ经过点(-2,0)时,同理可求出MP与x轴交点.
解答 解:(1)由抛物线y=ax2-2ax-4,
得B(0,-4),OB=4.
∵OA=OB=4,且点A在x轴正半轴上,
∴A(4,0).
将A(4,0)代入y=ax2-2ax-4,得
16a-8a-4=0,
解得a=$\frac{1}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-x-4;
(2)∵OA=OB=4,∠AOB=90°,
∴∠OAB=∠OBA=45°,AB=4$\sqrt{2}$,
∴∠ADM+∠AMD=135°,AM=BM=2$\sqrt{2}$.
∵∠CMD=45°,
∴∠AMD+∠BMC=135°,
∴∠ADM=∠BMC,
∴△ADM∽△BMC,
∴$\frac{BC}{AM}$=$\frac{BM}{AD}$.
∵AD=m,BC=n,
∴$\frac{n}{2\sqrt{2}}$=$\frac{2\sqrt{2}}{m}$,
∴n=$\frac{8}{m}$,
∴n与m之间的函数关系式为n=$\frac{8}{m}$;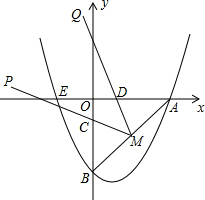 (3)设抛物线y=$\frac{1}{2}$x2-x-4与x轴另一个交点为E,
(3)设抛物线y=$\frac{1}{2}$x2-x-4与x轴另一个交点为E,
令y=0,得$\frac{1}{2}$x2-x-4=0,
解得x1=4,x2=-2,
∴点E的坐标为(-2,0).
∵A(4,0),B(0,-4),M为AB的中点,
∴M的坐标为(2,-2).
①当MP经过点(-2,0)时,
设直线PM的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{-2m+n=0}\\{2m+n=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=-1}\end{array}\right.$,
∴直线PM的解析式为y=-$\frac{1}{2}$x-1.
当x=0时,y=-1,
∴点C的坐标为(0,-1),
∴n=BC=-1-(-4)=3,
∴m=$\frac{8}{3}$,即AD=$\frac{8}{3}$,
∴OD=4-$\frac{8}{3}$=$\frac{4}{3}$,
∴MQ与x轴交点为($\frac{4}{3}$,0);
②当MQ经过点(-2,0)时,
同理可得:MP与x轴交点为(8,0).
点评 本题主要考查了运用待定系数法求直线与抛物线的解析式、直线与抛物线上点的坐标特征、等腰直角三角形的性质、相似三角形的判定与性质、勾股定理、中点坐标公式等知识,证到△ADM∽△BMC是解决第(2)小题的关键,运用(2)中的结论是解决第(3)小题的关键.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案

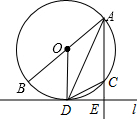 如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.
如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.