题目内容
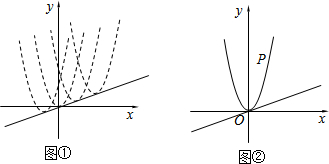
12.已知二次函数y=2x2+bx-1.(1)求证:无论b取什么值,二次函数y=2x2+bx-1图象与x轴必有两个交点.
(2)若两点P(-3,m)和Q(1,m)在该函数图象上.
①求b、m的值;
②将二次函数图象向上平移多少单位长度后,得到的函数图象与x轴只有一个公共点?
分析 (1)先计算判别式的值,再利用非负数的性质可判断△=>0,然后根据判别式的意义可判断抛物线与x轴必有两个交点;
(2)①先利用抛物线的对称性可确定抛物线的对称轴方程,从而可求出b的值,然后计算自变量为1所对应的函数值即可得到m的值;
②设平移后抛物线的关系式为y=2x2+4x-1+k,根据判别式的意义△=0得到关于k的方程,然后解方程求出k的值即可判断抛物线平移的距离.
解答 (1)证明:∵△=b2-4×2×(-1)=b2+8>0,
∴无论b取何值时,二次函数y=2x2+b x-1图象与x轴必有两个交点;
(2)解:①∵点P、Q是二次函数y=2x2+bx-1图象上的两点,且两点纵坐标都为m
∴点P、Q关于抛物线对称轴对称,
∴抛物线对称轴是直线x=-1,
∴-$\frac{b}{2×2}$=-1,解得b=4,
∴抛物线解析式为y=2x2+4x-1,
当x=1时,m=2×12+4×1-1=5;
②设平移后抛物线的关系式为y=2x2+4x-1+k,
∵平移后的图象与x轴仅有一个交点,
∴△=16+8-8 k=0,解得k=3,
即将二次函数图象向上平移3个单位时,函数图象与x轴仅有一个公共点.
点评 本题考查了二次函数与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
2.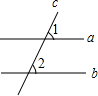 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
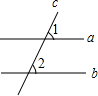 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
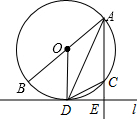 如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.
如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.