题目内容
3.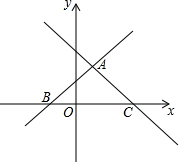 如图,在平面直角坐标系xOy中,直线y=x+1与y=-$\frac{3}{4}$x+3交于点A,且分别交x轴于点B和点C.
如图,在平面直角坐标系xOy中,直线y=x+1与y=-$\frac{3}{4}$x+3交于点A,且分别交x轴于点B和点C.(1)求点A、B、C的坐标;
(2)点D是直线AC上的一个动点,当△CBD为等腰三角形时,求满足条件的第四象限点D的坐标.
分析 (1)在两直线解析式中分别令y=0,求得相应的x的值,可求得B、C两点的坐标,联立两直线方程可求得A点坐标;
(2)由条件可得到BD=CD,设出D点坐标,过D作DM⊥x轴于点M,可表示出MC、DC,由勾股定理可得到关于x的方程,可求得D点坐标.
解答 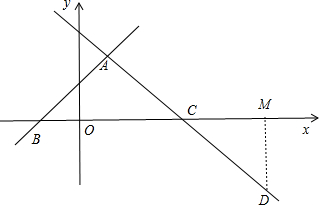 解:
解:
(1)在y=x+1中,令y=0可得x=-1,
∴B点坐标为(-1,0),
在y=-$\frac{3}{4}$x+3中,令y=0可得0=-$\frac{3}{4}$x+3,解得x=4,
∴C点坐标为(4,0),
联立两直线方程可得$\left\{\begin{array}{l}{y=x+1}\\{y=-\frac{3}{4}x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{8}{7}}\\{y=\frac{15}{7}}\end{array}\right.$,
∴A点坐标为($\frac{8}{7}$,$\frac{15}{7}$);
(2)当△CBD为等腰三角形,点D在第四象限时,∠BCD为钝角,则BC=CD.
设点D的坐标为(x,y),由(1)得B(-1,0),C(4,0),
∴BC=5.
如图,过D作DM⊥x轴于点M,则DM2+CM2=CD2,
∵MC=x-4,DM=|-$\frac{3}{4}$x+3|,DC=5,
∴(x-4)2+(-$\frac{3}{4}$x+3)2=52,
解得x=8或x=0(舍去),
此时y=-$\frac{3}{4}$×8+3=-3,
∴D点坐标为(8,-3).
点评 本题主要考查一次函数的交点,掌握两函数的交点坐标为对应方程组的解是解题的关键,在(2)中注意等腰三角形性质的应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
13.-2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
14.下列四个算式中,有一个算式与其他三个算式的计算结果符号不同,则该算式是( )
| A. | (-2013)2 | B. | -20132 | C. | (-2013)3 | D. | -|-2013| |
18.已知:在平面直角坐标系中,菱形ABCD三个顶点的坐标分别是A(-2,0)、B(0,1)、C(2,0),则点D的坐标是( )
| A. | (-4,-1) | B. | (4,-1) | C. | (0,-1) | D. | (0,-2) |
15.下列关于二次函数y=-(x-3)2+$\frac{1}{2}$的说法,错误的是( )
| A. | 其对称轴为x=3 | B. | 其图象的顶点坐标为(3,$\frac{1}{2}$) | ||
| C. | 其图象开口方向向下 | D. | 其图象与y轴的交点坐标为(0,$\frac{1}{2}$) |
 .
.