题目内容
8．
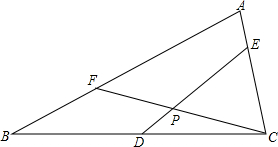如图，已知3AE=EC，2BF=AF，D为BC的中点，求EP：DP的值．
分析 连接PA、PB，根据题意设出各个三角形的面积，列式求出x和y的关系，根据等高的三角形的面积之比等于底的比求出EP：DP的值．
解答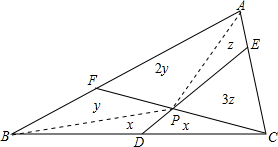 
解：连接PA、PB，
根据3AE=EC，2BF=AF，D为BC的中点，
如图设出各个部分的面积，
因为△ACF的面积=△BCF的面积的2倍，
所以2y+z+3z=2（x+x+y），
解得，x=z，
则EP：DP=3z：x=3：1．
点评 本题考查的是平行线分线段定理的应用，掌握等高的三角形的面积之比等于底的比是解题的关键．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
18．已知：在平面直角坐标系中，菱形ABCD三个顶点的坐标分别是A（-2，0）、B（0，1）、C（2，0），则点D的坐标是（ ）
| A． | （-4，-1） | B． | （4，-1） | C． | （0，-1） | D． | （0，-2） |
已知：如图，E，F是?ABCD的对角线AC上的两点，BE∥DF，求证：AF=CE．
16．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{9}$ | B． | $\sqrt{10}$ | C． | $\sqrt{20}$ | D． | $\sqrt{\frac{1}{3}}$ |
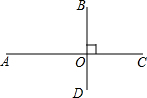如图，已知线段AC、BD相互垂直，垂足为O，且OA＞OC，OB＞OD．