题目内容
10.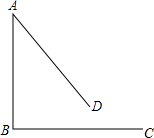 已知:AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.
已知:AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.(1)如图,①补全图形;②求∠AEC的度数;
(2)若AE=$\sqrt{2}$,CE=$\sqrt{3}$-1,请写出求α度数的思路.(可以不写出计算结果)
分析 (1)①作CF⊥BD并延长CF到E使EF=CF,如图,
②连结BE,如图,利用对称的性质得BE=BC,则∠BEC=∠C,则根据三角形内角和可计算出∠BEC=90°-$\frac{1}{2}$∠EBC,同样可得∠BEA=90°-$\frac{1}{2}$∠ABE,于是得到∠AEC=∠BEC+∠BEA=180°-$\frac{1}{2}$(∠EBC+∠ABE)=135°;
(2)作AH⊥CE于H,AG⊥BD于G,如图,先证明△AHE为等腰直角三角形,则AH=HE=$\frac{\sqrt{2}}{2}$AE=1,再利用对称的性质得CF=EF=$\frac{1}{2}$CE=$\frac{\sqrt{3}-1}{2}$,则HF=HE+EF=$\frac{\sqrt{3}+1}{2}$,接着利用四边形AGFH为矩形得到AG=HF=$\frac{\sqrt{3}+1}{2}$,然后根据旋转的性质得AB=AD,∠BAD=α,再证明△ABD≌△BCE得到∠CBE=∠BAD=α,AG=BF=$\frac{\sqrt{3}+1}{2}$,利用勾股定理计算出BE=$\sqrt{2}$,则可判断△ABE为等边三角形,所以∠ABE=60°,于是得到∠α=30°.
解答 解:(1)①如图,
②连结BE,如图,
∵点C关于直线BD的对称点为E,
∴BE=BC,
∴∠BEC=∠C,
∴∠BEC=$\frac{1}{2}$(180°-∠EBC)=90°-$\frac{1}{2}$∠EBC,
∵BA=BC,
∴BA=BE,
∴∠BAE=∠BEA,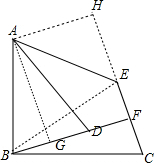
∴∠BEA=$\frac{1}{2}$(180°-∠ABE)=90°-$\frac{1}{2}$∠ABE,
∴∠AEC=∠BEC+∠BEA=90°-$\frac{1}{2}$∠EBC+90°-$\frac{1}{2}$∠ABE=180°-$\frac{1}{2}$(∠EBC+∠ABE)=180°-$\frac{1}{2}$×90°=135°;
(2)作AH⊥CE于H,AG⊥BD于G,如图,
∵∠AEC=135°,
∴∠AEH=45°,
∴△AHE为等腰直角三角形,
∴AH=HE=$\frac{\sqrt{2}}{2}$AE=1,
∵点C关于直线BD的对称点为E,
∴CF=EF=$\frac{1}{2}$CE=$\frac{\sqrt{3}-1}{2}$,
∴HF=HE+EF=1+$\frac{\sqrt{3}-1}{2}$=$\frac{\sqrt{3}+1}{2}$,
易得四边形AGFH为矩形,
∴AG=HF=$\frac{\sqrt{3}+1}{2}$,
∵线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD,
∴AB=AD,∠BAD=α,
∵∠ABD+∠CBF=90°,∠CBF+∠C=90°,
∴∠ABD=∠C,
∴△ABD≌△BCE,
∴∠CBE=∠BAD=α,AG=BF=$\frac{\sqrt{3}+1}{2}$,
在Rt△BFE中,BE=$\sqrt{B{F}^{2}+E{F}^{2}}$=$\sqrt{(\frac{\sqrt{3}+1}{2})^{2}+(\frac{\sqrt{3}-1}{2})^{2}}$=$\sqrt{2}$,
∴BE=AB=AE=$\sqrt{2}$,
∴△ABE为等边三角形,
∴∠ABE=60°,
∴∠CBE=30°,
∴∠α=30°.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了对称的性质和等边三角形的判定与性质.


| A. | 2 | B. | 8 | C. | $\sqrt{8}$ | D. | $\sqrt{18}$ |
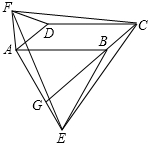 如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:
如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论: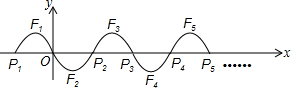 如图,在平面直角坐标系xOy中,二次函数y=-x2-2x图象位于x轴上方的部分记作F1,与x轴交于点P1和O;F2与F1关于点O对称,与x轴另一个交点为P2;F3与F2关于点P2对称,与x轴另一个交点为P3;….这样依次得到F1,F2,F3,…,Fn,则Fn的顶点坐标为[2n-3,(-1)n+1](n为正整数,用含n的代数式表示).
如图,在平面直角坐标系xOy中,二次函数y=-x2-2x图象位于x轴上方的部分记作F1,与x轴交于点P1和O;F2与F1关于点O对称,与x轴另一个交点为P2;F3与F2关于点P2对称,与x轴另一个交点为P3;….这样依次得到F1,F2,F3,…,Fn,则Fn的顶点坐标为[2n-3,(-1)n+1](n为正整数,用含n的代数式表示).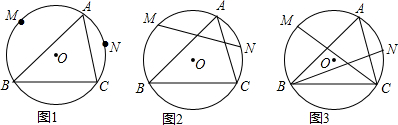

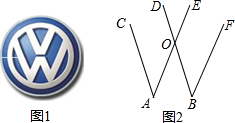 如图,图1是大众汽车的图标,图2反映其中直线间的关系,且AC∥BD,AE∥BF.
如图,图1是大众汽车的图标,图2反映其中直线间的关系,且AC∥BD,AE∥BF.