题目内容
18.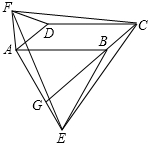 如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:
如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:①CG⊥AE;
②△CDF≌△EBC;
③∠CDF=∠EAF;
④△ECF是等边三角形.
其中一定正确的是②③④.(把正确结论的序号都填上)
分析 根据等边三角形的性质,只有∠ABC=150°时,CG⊥AE.根据平行四边形的对角相等,等边三角形的每一个角都是60°表示出∠CDF=∠EBC,平行四边形的对边相等,等边三角形的三条边都相等可得CD=EB,DE=BC,然后利用“边角边”证明△CDF和△EBC全等,判定②正确;再表示出∠EAF,可得∠CDF=∠EAF,判定③正确;同理求出△CDF和△EAF全等,根据全等三角形对应边相等可得CE=CF=EF,判定△ECF是等边三角形,判定④正确;
解答 解:在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段
∴如果CG⊥AE,则G是AE的中点,∠ABG=30°,∠ABC=150°,题目缺少这个条件,CG⊥AE不能求证,故①错误;
∵△ABE、△ADF是等边三角形
∴FD=AD,BE=AB
∵AD=BC,AB=DC
∴FD=BC,BE=DC
∵∠B=∠D,∠FDA=∠ABE
∴∠CDF=∠EBC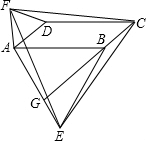
∴△CDF≌△EBC,故②正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°-∠CDA)=300°-∠CDA,
∠FDC=360°-∠FDA-∠ADC=300°-∠CDA,
∴∠CDF=∠EAF,故③正确;
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC,
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故④正确;
正确的有②③④,
故答案为:②③④.
点评 本题考查了全等三角形的判定、等边三角形的判定和性质、平行四边形的性质等知识,综合性强.考查学生综合运用数学知识的能力.

练习册系列答案
相关题目
14. 一元一次不等式的解集在数轴上表示为如图,则它的解集是( )
一元一次不等式的解集在数轴上表示为如图,则它的解集是( )
 一元一次不等式的解集在数轴上表示为如图,则它的解集是( )
一元一次不等式的解集在数轴上表示为如图,则它的解集是( )| A. | x≥-2 | B. | x>-2 | C. | x≤-2 | D. | x<-2 |
9. 如图,点A表示的实数是( )
如图,点A表示的实数是( )
 如图,点A表示的实数是( )
如图,点A表示的实数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $-\sqrt{5}$ | D. | $-\sqrt{3}$ |
3.已知一个直角三角形的两条边长分别是6和8,则第三边长是( )
| A. | 10 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10或2$\sqrt{7}$ |
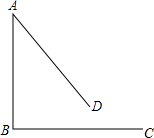 已知:AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.
已知:AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.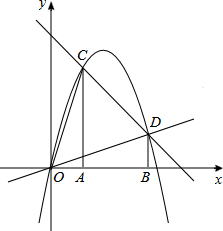 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点. 如图,将三角板的直角顶点放在直尺的一边上,若∠1=70°,则∠2的度数为20°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=70°,则∠2的度数为20°.