Question

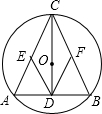如图，⊙O是△ABC的外接圆，圆心O在△ABC的高CD上，点E、F分别是边AC和BC的中点，请你判断四边形CEDF的形状，并说明理由．

Answer 1

考点：三角形的外接圆与外心,三角形中位线定理,菱形的判定

专题：

分析：由垂径定理知，点D是AB的中点，有AD=BD，可证△CAD≌△CBD，可得AC=BC；由E，F分别为AC，BC的中点，D为AB中点，得DF=CE=

1

2

AC，DE=CF=

1

2

BC，即DE=DF=CE=CF，从而可得四边形CEDF为菱形．

解答：解：四边形CEDF为菱形．
证明：∵AB为弦，CD为直径所在的直线且AB⊥CD，
∴AD=BD，
又∵CD=CD，
∴△CAD≌△CBD，
∴AC=BC；
又∵E，F分别为AC，BC的中点，D为AB中点，
∴DF=CE=

1

2

AC，DE=CF=

1

2

BC，
∴DE=DF=CE=CF，
∴四边形CEDF为菱形．

点评：本题考查了垂径定理、三角形全等、三角形中位线的性质以及菱形的判定．