题目内容
 已知双曲线y=
已知双曲线y=| m |
| x |
| 4 |
| 3 |
| m |
| x |
(1)求出反比例函数与一次函数的解析式;
(2)连接EF,求△AEF的面积.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)作AB⊥OE于E点,根据等腰三角形的性质得OB=EB,利用正切的定义得tan∠AOB=
=
,设AB=4x,则OB=3x,根据勾股定理得OA=5x,则x=1,于是AB=4,OB=3,
得到A(-3,4),把它代入反比例函数解析式求出k,接着确定F点坐标,然后利用待定系数法确定一次函数的解析式;
(2)先求出一次函数与x轴的交点坐标C(3,0),再根据B点坐标确定E点坐标,然后利用S△AEF=S△AEC+S△FEC进行计算.
| AB |
| OB |
| 4 |
| 3 |
得到A(-3,4),把它代入反比例函数解析式求出k,接着确定F点坐标,然后利用待定系数法确定一次函数的解析式;
(2)先求出一次函数与x轴的交点坐标C(3,0),再根据B点坐标确定E点坐标,然后利用S△AEF=S△AEC+S△FEC进行计算.
解答:解:(1)作AB⊥OE于B点,如图,
∵AO=AE,
∴OB=EB,
在RtAOB中
∵tan∠AOB=
=
,
设AB=4x,则OB=3x,
∴OA=
=5x,
而AO=5,
∴x=1,
∴AB=4,OB=3,
∴A(-3,4),
把A(-3,4)代入y=
得m=-3×4=-12,
∴反比例函数的解析式为:y=-
,
把F(6,n)代入y=-
得6n=-12,解得n=-2,
∴F点坐标为(6,-2),
把A(-3,4)、F(6,-2)代入y=kx+b得
,解得
,
故一次函数的解析式为:y=-
x+2;
(2)如图,C点坐标为(3,0),E点坐标为(-6,0),
S△AEF=S△AEC+S△FEC=
×9×4+
×9×2=18+9=27.
∵AO=AE,
∴OB=EB,
在RtAOB中
∵tan∠AOB=
| AB |
| OB |
| 4 |
| 3 |
设AB=4x,则OB=3x,
∴OA=
| AB2+OB2 |

而AO=5,
∴x=1,
∴AB=4,OB=3,
∴A(-3,4),
把A(-3,4)代入y=
| m |
| x |
∴反比例函数的解析式为:y=-
| 12 |
| x |
把F(6,n)代入y=-
| 12 |
| x |
∴F点坐标为(6,-2),
把A(-3,4)、F(6,-2)代入y=kx+b得
|
|
故一次函数的解析式为:y=-
| 2 |
| 3 |
(2)如图,C点坐标为(3,0),E点坐标为(-6,0),
S△AEF=S△AEC+S△FEC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式.也考查了待定系数法求函数的解析式、等腰三角形的性质以及三角形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各数中,无理数是( )
| A、0 | ||
B、
| ||
C、
| ||
| D、-3.14 |
⊙O1的半径为1,⊙O2的半径为8,两圆的圆心距为7,则两圆的位置关系为( )
| A、相交 | B、内切 | C、相切 | D、外切 |
不等式
的解集是( )
|
| A、-6<x<2 |
| B、-6<x≤2 |
| C、-6≤x<2 |
| D、-2≤x≤6 |
 如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF.
如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF.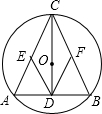 如图,⊙O是△ABC的外接圆,圆心O在△ABC的高CD上,点E、F分别是边AC和BC的中点,请你判断四边形CEDF的形状,并说明理由.
如图,⊙O是△ABC的外接圆,圆心O在△ABC的高CD上,点E、F分别是边AC和BC的中点,请你判断四边形CEDF的形状,并说明理由.