题目内容
 如图,已知梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且∠ACB=∠DBA.
如图,已知梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且∠ACB=∠DBA.(1)求证:△AOD∽△BAD;
(2)若△AOD的面积为3,AB=3OA,求△AOB的面积.
考点:相似三角形的判定与性质,梯形
专题:
分析:(1)根据利用平行线的性质得出∠DAC=∠ACB,进而利用相似三角形的判定得出即可;
(2)利用相似三角形的性质得出
=(
)2=
,进而求出即可.
(2)利用相似三角形的性质得出
| S△ABD |
| S△AOD |
| 3 |
| 1 |
| 9 |
| 1 |
解答:(1)证明:∵梯形ABCD中,AD∥BC,
∴∠DAC=∠ACB,
∵∠ACB=∠DBA,
∴∠DAC=∠DBA,
∵∠ADO=∠BDA,
∴△AOD∽△BAD;
(2)解:∵△AOD∽△BAD,AB=3OA,
∴
=
,
∴
=(
)2=
,
∵△AOD的面积为3,
∴S△ABD=3×9=27,
∴△AOB的面积为:27-3=24.
∴∠DAC=∠ACB,
∵∠ACB=∠DBA,
∴∠DAC=∠DBA,
∵∠ADO=∠BDA,
∴△AOD∽△BAD;
(2)解:∵△AOD∽△BAD,AB=3OA,
∴
| AB |
| AO |
| 3 |
| 1 |
∴
| S△ABD |
| S△AOD |
| 3 |
| 1 |
| 9 |
| 1 |
∵△AOD的面积为3,
∴S△ABD=3×9=27,
∴△AOB的面积为:27-3=24.
点评:此题主要考查了相似三角形的判定与性质,根据已知得出
=(
)2是解题关键.
| S△ABD |
| S△AOD |
| 3 |
| 1 |

练习册系列答案
相关题目
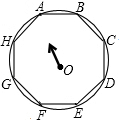 如图,多边形ABCDEFGH为⊙O的内接正八边形,图中箭头正好指向点A,当箭头绕着点O逆时针旋转270°时,箭头应正好指向( )
如图,多边形ABCDEFGH为⊙O的内接正八边形,图中箭头正好指向点A,当箭头绕着点O逆时针旋转270°时,箭头应正好指向( )| A、点G | B、点E | C、点D | D、点C |
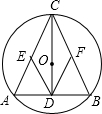 如图,⊙O是△ABC的外接圆,圆心O在△ABC的高CD上,点E、F分别是边AC和BC的中点,请你判断四边形CEDF的形状,并说明理由.
如图,⊙O是△ABC的外接圆,圆心O在△ABC的高CD上,点E、F分别是边AC和BC的中点,请你判断四边形CEDF的形状,并说明理由. 如图,在平面直角坐标系中,O为坐标原点,正方形OABC的边长是2,且∠COx=30°,求点A、B、C的坐标.
如图,在平面直角坐标系中,O为坐标原点,正方形OABC的边长是2,且∠COx=30°,求点A、B、C的坐标. 如图,⊙O的直径AB=10cm,C是⊙O上一点,作OD∥AC交⊙O于点D,交BC于点E,DE=2cm,则弦AC=
如图,⊙O的直径AB=10cm,C是⊙O上一点,作OD∥AC交⊙O于点D,交BC于点E,DE=2cm,则弦AC= 如图,PA为⊙0的切线,A为切点,过A作O的垂线AB,垂足为点C,交⊙O于点B.
如图,PA为⊙0的切线,A为切点,过A作O的垂线AB,垂足为点C,交⊙O于点B.