题目内容
 实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )| A、2a+b | B、-b |
| C、-2a-b | D、b |
考点:整式的加减,绝对值,实数与数轴
专题:计算题
分析:根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,合并即可得到结果.
解答:
解:根据数轴上点的位置得:b<0<a,且|b|>|a|,
∴a+b<0,
则原式=-a-b-a=-2a-b,
故选C.
∴a+b<0,
则原式=-a-b-a=-2a-b,
故选C.
点评:此题考查了整式的加减,绝对值,实数与数轴,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
已知|a|=5,|b|=8,且满足a+b<0,则a-b的值为( )
| A、-13 | B、13 |
| C、3或13 | D、13或-13 |
下面用数学语言叙述代数式
-b,其中表达不正确的是( )
| 1 |
| a |
| A、比a的倒数小b的数 |
| B、1除以a的商与b的相反数的差 |
| C、1除以a的商与b的相反数的和 |
| D、b与a的倒数的差的相反数 |
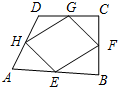 如图,已知四边形EFGH是四边形ABCD的中点四边形,若四边形EFGH是菱形,则原四边形ABCD可能为( )
如图,已知四边形EFGH是四边形ABCD的中点四边形,若四边形EFGH是菱形,则原四边形ABCD可能为( )| A、直角梯形 |
| B、平行四边形 |
| C、等腰梯形 |
| D、对角线互相垂直的四边形 |
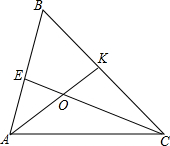 如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.
如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE. 如图,已知AB=AD,AC=AE,∠1=∠2
如图,已知AB=AD,AC=AE,∠1=∠2 AB=AC,∠1=∠2,∠3=∠4,求证:BE=CF.
AB=AC,∠1=∠2,∠3=∠4,求证:BE=CF.