题目内容
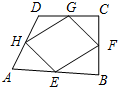 如图,已知四边形EFGH是四边形ABCD的中点四边形,若四边形EFGH是菱形,则原四边形ABCD可能为( )
如图,已知四边形EFGH是四边形ABCD的中点四边形,若四边形EFGH是菱形,则原四边形ABCD可能为( )| A、直角梯形 |
| B、平行四边形 |
| C、等腰梯形 |
| D、对角线互相垂直的四边形 |
考点:中点四边形
专题:
分析:添加的条件应为:AC=BD,把AC=BD作为已知条件,根据三角形的中位线定理可得,HG平行且等于AC的一半,EF平行且等于AC的一半,根据等量代换和平行于同一条直线的两直线平行,得到HG和EF平行且相等,所以四边形EFGH为平行四边形,又EH等于BD的一半且AC=BD,所以得到所证四边形的邻边EH与HG相等,所以四边形EFGH为菱形.
解答:
解:添加的条件应为:AC=BD.
理由如下:∵E,F,G,H分别是边AB、BC、CD、DA的中点,
∴在△ADC中,HG为△ADC的中位线,
∴HG∥AC且HG=
AC;
同理EF∥AC且EF=
AC,
同理可得EH=
BD,
则HG∥EF且HG=EF,
∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,
∴四边形EFGH为菱形.
当AC=BD时,四边形ABCD可能是矩形,也可能是等腰梯形.
故选:C.
理由如下:∵E,F,G,H分别是边AB、BC、CD、DA的中点,
∴在△ADC中,HG为△ADC的中位线,
∴HG∥AC且HG=
| 1 |
| 2 |
同理EF∥AC且EF=
| 1 |
| 2 |
同理可得EH=
| 1 |
| 2 |
则HG∥EF且HG=EF,
∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,
∴四边形EFGH为菱形.
当AC=BD时,四边形ABCD可能是矩形,也可能是等腰梯形.
故选:C.
点评:此题考查学生灵活运用三角形的中位线定理,平行四边形的判断及菱形的判断进行证明,是一道综合题.

练习册系列答案
相关题目
 实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )| A、2a+b | B、-b |
| C、-2a-b | D、b |
2014年10月7日21时49分,云南省普洱市景谷发生6.6级地震,截至9日11时,地震造成普洱市、临沧市共12个县区30.88万人不同程度受灾,为支援灾区,某市向普洱市派出11组医疗救援队(每组6人)和12组搜救队(每组15人),后因余震,从派去普洱市的医疗救援队和搜救队中各抽出5组派往临沧市,则从该市派去参加救援的人在普洱市还剩( )
| A、151人 | B、141人 |
| C、131人 | D、105人 |
下列语句是命题的是( )
| A、作线段AB的中点 |
| B、作线段AB的垂直平分线 |
| C、等角的补角相等吗? |
| D、对顶角不相等 |

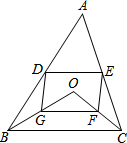 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.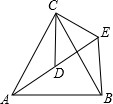 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.