题目内容
7.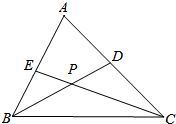 如图,在△ABC中,BD、CE分别是∠ABC,∠ACB的平分线.
如图,在△ABC中,BD、CE分别是∠ABC,∠ACB的平分线.(1)若∠ABC=60°,∠ACB=40°时,求∠BPC的度数.
(2)当∠A=80°时,求∠BPC的度数.
(3)当∠A=x时,用含x代数式表示∠BPC的度数.
分析 (1)先根据角平分线的性质得出∠PBC与∠PCB的度数,再根据三角形内角和定理即可得出结论;
(2)先根据∠A=80°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠PBC+∠PCB的度数,根据三角形内角和定理即可得出结论;
(3)根据∠A=x求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠PBC+∠PCB的度数,根据三角形内角和定理即可得出结论.
解答 解:(1)∵在△ABC中,∠ABC=60°,∠ACB=80°,BD和CE分别平分∠ABC和∠ACB,
∴∠PBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠PCB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×40°=20°,
∴∠BPC=180°-∠PBC-∠PCB=180°-30°-20°=130°;
(2)∵在△ABC中,∠A=80°,BD和CE分别平分∠ABC和∠ACB,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-80°)=50°,
∴∠BPC=180°-50°=130°;
(3)在△ABC中,∠A=x,BD和CE分别平分∠ABC和∠ACB,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-x)=90°-$\frac{1}{2}$x,
∴∠BPC=180°-(90°-x)=90°+$\frac{1}{2}$x.
点评 本题考查的是三角形内角和定理,角平分线的性质,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
 如图,已知直线AB∥DF,∠D+∠B=180°,
如图,已知直线AB∥DF,∠D+∠B=180°,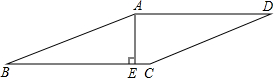 如图,在菱形ABCD中,已知AE⊥BC于点E,EC=1,且AE:BE=5:2,求四边形ABCD的周长.
如图,在菱形ABCD中,已知AE⊥BC于点E,EC=1,且AE:BE=5:2,求四边形ABCD的周长.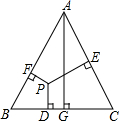 如图,已知等边三角形ABC中,AG⊥BC,PD⊥BC,PE⊥AC,PF⊥AB.求证:PD+PE+PF=AG.
如图,已知等边三角形ABC中,AG⊥BC,PD⊥BC,PE⊥AC,PF⊥AB.求证:PD+PE+PF=AG. 如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )
如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )